

| 5 |
| 3 |
|
|
| 5 |
| 3 |
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 ,
, ,
,
 ≌
≌ ;
; ,
, ,
, ,
, 的度數
的度數 繞點A逆時針旋轉
繞點A逆時針旋轉 度(
度( ),問當
),問當 為多少度時,直線CE分別與
為多少度時,直線CE分別與 的三邊所在的直線垂直?(請直接寫出答案)。
的三邊所在的直線垂直?(請直接寫出答案)。 繞點A逆時針旋轉后得到
繞點A逆時針旋轉后得到 ,并使點D,E,A三點在同一條直線上,若
,并使點D,E,A三點在同一條直線上,若 ,連接CD,若
,連接CD,若 的面積為6cm2,你能求出四邊形ABDC的面積嗎?若能,請求出來;若不能,請你說明理由。
的面積為6cm2,你能求出四邊形ABDC的面積嗎?若能,請求出來;若不能,請你說明理由。
查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江省寧波地區初一第二學期期中考試數學卷(帶解析) 題型:解答題
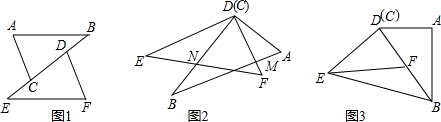
如圖1所示,已知在△ABD和△AEC中, ,
, ,
,
【小題1】如圖1,試說明: ≌
≌ ;
;
【小題2】如圖1,若 ,
, ,
, ,
,
①試求: 的度數
的度數
②將 繞點A逆時針旋轉
繞點A逆時針旋轉 度(
度( ),問當
),問當 為多少度時,直線CE分別與
為多少度時,直線CE分別與 的三邊所在的直線垂直?(請直接寫出答案)。
的三邊所在的直線垂直?(請直接寫出答案)。
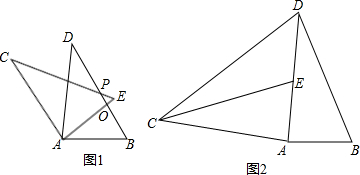
【小題3】如圖2將 繞點A逆時針旋轉后得到
繞點A逆時針旋轉后得到 ,并使點D,E,A三點在同一條直線上,若
,并使點D,E,A三點在同一條直線上,若 ,連接CD,若
,連接CD,若 的面積為6cm2,你能求出四邊形ABDC的面積嗎?若能,請求出來;若不能,請你說明理由。
的面積為6cm2,你能求出四邊形ABDC的面積嗎?若能,請求出來;若不能,請你說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com