
閱讀以下的材料:
如果兩個正數![]() ,即
,即![]() ,有下面的不等式:
,有下面的不等式:
![]() 當且僅當
當且僅當![]() 時取到等號
時取到等號
我們把![]() 叫做正數
叫做正數![]() 的算術平均數,把
的算術平均數,把![]() 叫做正數
叫做正數![]() 的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數。它在數學中有廣泛的應用,是解決最值問題的有力工具。下面舉一例子:
的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數。它在數學中有廣泛的應用,是解決最值問題的有力工具。下面舉一例子:
例:已知![]() ,求函數
,求函數![]() 的最小值。
的最小值。
解:令![]() ,則有
,則有![]() ,得
,得![]() ,當且僅當
,當且僅當![]() 時,即
時,即![]() 時,函數有最小值,最小值為
時,函數有最小值,最小值為![]() 。
。
根據上面回答下列問題
① 已知![]() ,則當
,則當![]() 時,函數
時,函數![]() 取到最小值,最小值
取到最小值,最小值
為 ;
② 用籬笆圍一個面積為![]() 的矩形花園,問這個矩形的長、寬各為多少時,所
的矩形花園,問這個矩形的長、寬各為多少時,所
用的籬笆最短,最短的籬笆周長是多少;
③. 已知![]() ,則自變量
,則自變量![]() 取何值時,函數
取何值時,函數![]() 取到最大值,最大值為多少?
取到最大值,最大值為多少?
科目:初中數學 來源: 題型:閱讀理解
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| 4 |
| x |
| 4 |
| x |
| ab |
| 4 |
| x |
x•
|
| 4 |
| x |
| 3 |
| x |
| x |
| x2-2x+9 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
閱讀以下的材料:
如果兩個正數![]() ,即
,即![]() ,有下面的不等式:
,有下面的不等式:
![]() 當且僅當
當且僅當![]() 時取到等號
時取到等號
我們把![]() 叫做正數
叫做正數![]() 的算術平均數,把
的算術平均數,把![]() 叫做正數
叫做正數![]() 的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數。它在數學中有廣泛的應用,是解決最值問題的有力工具。下面舉一例子:
的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數。它在數學中有廣泛的應用,是解決最值問題的有力工具。下面舉一例子:
例:已知![]() ,求函數
,求函數![]() 的最小值。
的最小值。
解:令![]() ,則有
,則有![]() ,得
,得![]() ,當且僅當
,當且僅當![]() 時,即
時,即![]() 時,函數有最小值,最小值為
時,函數有最小值,最小值為![]() 。
。
根據上面回答下列問題
① 已知![]() ,則當
,則當![]() 時,函數
時,函數![]() 取到最小值,最小值
取到最小值,最小值
為 ;
② 用籬笆圍一個面積為![]() 的矩形花園,問這個矩形的長、寬各為多少時,所
的矩形花園,問這個矩形的長、寬各為多少時,所
用的籬笆最短,最短的籬笆周長是多少;
③. 已知![]() ,則自變量
,則自變量![]() 取何值時,函數
取何值時,函數![]() 取到最大值,最大值為多少?
取到最大值,最大值為多少?
查看答案和解析>>
科目:初中數學 來源:2013年江蘇省鹽城市東臺實驗中學中考數學模擬試卷(6月份)(解析版) 題型:解答題
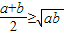 當且僅當a=b時取到等號
當且僅當a=b時取到等號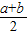 叫做正數a,b的算術平均數,把
叫做正數a,b的算術平均數,把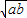 叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最大(小)值問題的有力工具,下面舉一例子:
叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最大(小)值問題的有力工具,下面舉一例子: 的最小值.
的最小值.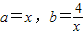 ,則有
,則有 ,得
,得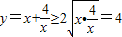 ,當且僅當
,當且僅當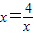 時,即x=2時,函數有最小值,最小值為2.
時,即x=2時,函數有最小值,最小值為2.查看答案和解析>>
科目:初中數學 來源:2013年浙江省寧波市中考數學模擬試卷(八)(解析版) 題型:解答題
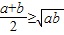 當且僅當a=b時取到等號
當且僅當a=b時取到等號 叫做正數a,b的算術平均數,把
叫做正數a,b的算術平均數,把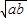 叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最大(小)值問題的有力工具,下面舉一例子:
叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最大(小)值問題的有力工具,下面舉一例子: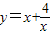 的最小值.
的最小值.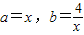 ,則有
,則有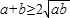 ,得
,得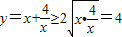 ,當且僅當
,當且僅當 時,即x=2時,函數有最小值,最小值為2.
時,即x=2時,函數有最小值,最小值為2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com