
某食品加工廠需要一批食品包裝盒,供應這種包裝盒有兩種方案可供選擇:
方案1:從包裝盒加工廠直接購買,購買所需的費用y1與包裝盒數x滿足如圖的函數關系。
方案2:租憑機器自己加工,所需費用y2(包括租憑機器的費用和生產包裝盒的費用)
與包裝盒數 滿足如圖的函數關系。
滿足如圖的函數關系。
根據圖象回答下列問題:
(1)方案1中每個包裝盒的價格是多少元?
(2)方案2中租憑機器的費用是多少元?生產一個包裝盒的費用是多少元?
(3)請分別求出y1,y2,與x的函數表達式
(4)如果你是決策者,你認為應該選擇哪種方案更省錢?并說明理由。
(1)5;(2)20000,2.5;(3)y1=5x,y2=2.5x+20000;(4)當x=8000時,兩種方案同樣省錢;當x<8000時,選擇方案一;當x>8000時,選擇方案二.
解析試題分析:(1)根據圖象1可知100個盒子共花費500元,據此可以求出盒子的單價;
(2)根據圖2可以知道租賃機器花費20000元,根據圖象所經過的點的坐標求出盒子的單價即可;
(3)根據圖象經過的點的坐標用待定系數法求得函數的解析式即可;
(4)求出當x的值為多少時,兩種方案同樣省錢,并據此分類討論最省錢的方案即可.
試題解析:(1)500÷100=5,
∴方案一的盒子單價為5元;
(2)根據函數的圖象可以知道租賃機器的費用為20000元,
盒子的單價為(30000-20000)÷4000=2.5,
故盒子的單價為2.5元;
(3)設圖象一的函數解析式為:y1=k1x,
由圖象知函數經過點(100,500),
∴500=100k1,
解得k1=5,
∴函數的解析式為y1=5x;
設圖象二的函數關系式為y2=k2x+b
由圖象知道函數的圖象經過點(0,20000)和(4000,30000)
∴ ,
,
解得:
∴函數的解析式為y2=2.5x+20000;
(4)令5x=2.5x+20000,
解得x=8000,
∴當x=8000時,兩種方案同樣省錢;
當x<8000時,選擇方案一;
當x>8000時,選擇方案二.
考點:一次函數的應用.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
如圖,△ABC三個頂點的坐標分別為A(2,3)、B(1,1)、C(5,1),先將△ABC作關于x軸的軸對稱圖形得到△A1B1C1,再將△A1B1C1向左平移5個單位得△A2B2C2.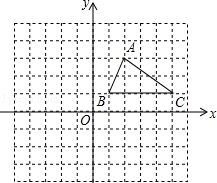
(1)分別畫出兩次變換的像△A1B1C1與△A2B2C2;
(2)求出邊AB所在直線的函數解析式,并判斷點C2是否在該直線上.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,二次函數 的圖象與x軸交于兩個不同的點A(﹣2,0)、B(4,0),與y軸交于點C(0,3),連接BC、AC,該二次函數圖象的對稱軸與x軸相交于點D.
的圖象與x軸交于兩個不同的點A(﹣2,0)、B(4,0),與y軸交于點C(0,3),連接BC、AC,該二次函數圖象的對稱軸與x軸相交于點D.
(1)求這個二次函數的解析式、
(2)點D的坐標及直線BC的函數解析式;
(3)點Q在線段BC上,使得以點Q、D、B為頂點的三角形與△ABC相似,求出點Q的坐標;
(4)在(3)的條件下,若存在點Q,請任選一個Q點求出△BDQ外接圓圓心的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,直線MN與x軸,y軸分別相交于A,C兩點,分別過A,C兩點作x軸,y軸的垂線相交于B點,且OA,OC(OA>OC)的長分別是一元二次方程x2﹣14x+48=0的兩個實數根.
(1)求C點坐標;
(2)求直線MN的解析式;
(3)在直線MN上存在點P,使以點P,B,C三點為頂點的三角形是等腰三角形,請直接寫出P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,某個體戶購進一批時令水果,20天銷售完畢.他將本次銷售情況進行了跟蹤記錄,根據所記錄的數據可繪制的函數圖象,其中日銷售量y(千克)與銷售時間x(天)之間的函數關系如圖甲所示,銷售單價p(元/千克)與銷售時間x(天)之間的函數關系如圖乙所示.
(1)直接寫出y與x之間的函數關系式;
(2)分別求出第10天和第15天的銷售金額;
(3)若日銷售量不低于24千克的時間段為“最佳銷售期”,則此次銷售過程中“最佳銷售期”共有多少天?在此期間銷售單價最高為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com