
 ,拋物線y=ax2+bx經過點A(4,0)與點(-2,6).
,拋物線y=ax2+bx經過點A(4,0)與點(-2,6).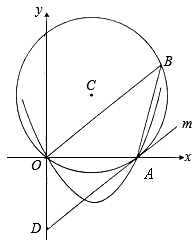
 x2-2x;(2)1.8;(3)(
x2-2x;(2)1.8;(3)( ,
,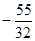 )
) 可得sin∠AOB=
可得sin∠AOB=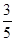 ,即可求得AE、OD的長,當PQ⊥AD時,OP=t,DQ=2t.則在Rt△ODF中,OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,再根據勾股定理求解;
,即可求得AE、OD的長,當PQ⊥AD時,OP=t,DQ=2t.則在Rt△ODF中,OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,再根據勾股定理求解; 可得直線OB的解析式為y=
可得直線OB的解析式為y= x,由直線l平行于OB,可設直線l解析式為y=
x,由直線l平行于OB,可設直線l解析式為y= x+b.點R既在直線l上,又在拋物線上,可得
x+b.點R既在直線l上,又在拋物線上,可得 x2-2x=
x2-2x= x+b,再根據直線l與拋物線有唯一交點R(相切),可得方程2x2-11x-4b=0有兩個相等的實數根,即可得到判別式△=0,從而可以求得結果.
x+b,再根據直線l與拋物線有唯一交點R(相切),可得方程2x2-11x-4b=0有兩個相等的實數根,即可得到判別式△=0,從而可以求得結果. ,解得a=
,解得a= ,b=-2
,b=-2 x2-2x;
x2-2x;

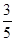 ,
,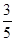 =2.4,
=2.4, =3.
=3.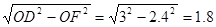 ,
,
 x,
x, x+b.
x+b. x2-2x=
x2-2x= x+b,化簡得:2x2-11x-4b=0.
x+b,化簡得:2x2-11x-4b=0. ,
, ,即xR=
,即xR=  ,
, xR2-2xR=
xR2-2xR=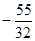
 ,
,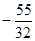 ).
).

 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 (
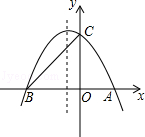
( )與y軸交于點A,其對稱軸與x軸交于點B。
)與y軸交于點A,其對稱軸與x軸交于點B。
 這一段位于直線l的上方,并且在
這一段位于直線l的上方,并且在 這一段位于直線AB的下方,求該拋物線的解析式。
這一段位于直線AB的下方,求該拋物線的解析式。查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 交
交 軸于點
軸于點 ,交
,交 軸于點
軸于點 ,拋物線
,拋物線 經過
經過 、
、 、
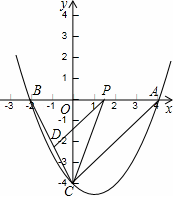
、 (1,0)三點.
(1,0)三點.
 的坐標為(-1,0),在直線
的坐標為(-1,0),在直線 上有一點
上有一點 ,使
,使 與
與 相似,求出點
相似,求出點 的坐標;
的坐標; 軸下方的拋物線上,是否存在點
軸下方的拋物線上,是否存在點 ,使
,使 的面積等于四邊形
的面積等于四邊形 的面積?如果存在,請求出點
的面積?如果存在,請求出點 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com