
已知拋物線 (m是常數,
(m是常數,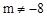 )與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,拋物線的頂點為C.
)與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,拋物線的頂點為C.
(1)此拋物線的解析式;
(2)求點A、B、C的坐標.
(1)y=x2-2x;(2)(0,0),(2,0),(1,-1).
解析試題分析:(1)根據已知條件知,該拋物線的對稱軸是x=1,然后利用拋物線對稱軸方程列出關于m的方程 ,則易求m的值;
,則易求m的值;
(2)根據(1)中的函數解析式知,分別求當x=0,y的值;當y=0時,x的值.
試題解析::(1)∵拋物線 (m為常數,m≠-8))的對稱軸為
(m為常數,m≠-8))的對稱軸為 ,而拋物線與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,
,而拋物線與x軸有兩個不同的交點A、B,點A、點B關于直線x=1對稱,
∴ ,解得m=-6.
,解得m=-6.
∴所求拋物經的解析式為y=x2-2x.
(2)當y=0時,x2-2x=0,解得x1=0,x2=2.
又y=x2-2x=(x-1)2-1,
∴點A、B、C的坐標.分別為(0,0),(2,0),(1,-1).
考點:1.二次函數的性質;2.拋物線與x軸的交點.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:解答題
某商店進了一批服裝,每件成本50元,如果按每件60元出售,可銷售800件,如果每件提價5元出售,其銷量將減少100件。
(1)求售價為70元時的銷售量及銷售利潤;
(2)求銷售利潤y(元)與售價x(元)之間的函數關系,并求售價為多少元時獲得最大利潤;
(3)如果商店銷售這批服裝想獲利12000元,那么這批服裝的定價是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某公司銷售一種新型節能電子小產品,現準備從國內和國外兩種銷售方案中選擇一種進行銷售:①若只在國內銷售,銷售價格y(元/件)與月銷量x(件)的函數關系式為y=- x+150,成本為20元/件,月利潤為W內(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,10≤a≤40),當月銷量為x(件)時,每月還需繳納
x+150,成本為20元/件,月利潤為W內(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,10≤a≤40),當月銷量為x(件)時,每月還需繳納 x2元的附加費,月利潤為W外(元).
x2元的附加費,月利潤為W外(元).
(1)若只在國內銷售,當x=1000(件)時,y= (元/件);
(2)分別求出W內、W外與x間的函數關系式(不必寫x的取值范圍);
(3)若在國外銷售月利潤的最大值與在國內銷售月利潤的最大值相同,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在直角梯形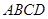 中,
中,  , 高
, 高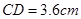 (如圖1). 動點
(如圖1). 動點 同時從點
同時從點 出發, 點
出發, 點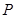 沿
沿 運動到點
運動到點 停止, 點
停止, 點 沿
沿 運動到點
運動到點 停止,兩點運動時的速度都是1cm/s,而當點
停止,兩點運動時的速度都是1cm/s,而當點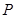 到達點
到達點 時,點
時,點 正好到達點
正好到達點 . 設
. 設 同時從點
同時從點 出發,經過的時間為
出發,經過的時間為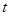 (s)時,
(s)時,  的面積為
的面積為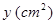 (如圖2). 分別以
(如圖2). 分別以 為橫、縱坐標建立直角坐標系, 已知點
為橫、縱坐標建立直角坐標系, 已知點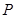 在
在 邊上從
邊上從 到
到 運動時,
運動時,  與
與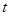 的函數圖象是圖3中的線段
的函數圖象是圖3中的線段 .
.

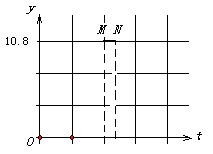
(圖1) (圖2) (圖3)
(1)分別求出梯形中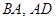 的長度;
的長度;
(2)分別寫出點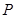 在
在 邊上和
邊上和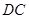 邊上運動時,
邊上運動時,  與
與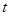 的函數關系式(注明自變量的取值范圍), 并在圖3中補全整個運動中
的函數關系式(注明自變量的取值范圍), 并在圖3中補全整個運動中 關于
關于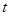 的函數關系的大致圖象.
的函數關系的大致圖象.
(3)問:是否存在這樣的t,使PQ將梯形ABCD的面積恰好分成1:6的兩部分?若存在,求出這樣的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線y=ax2+bx+c(a≠0)的頂點坐標為(4,﹣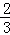 ),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
(1)求拋物線的解析式及A,B兩點的坐標;
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,請說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數y=x2+bx+c中,函數y與自變量x的部分對應值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
 ?
?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,某中學校園有一塊長為35m,寬為16m的長方形空地,其中有一面已經鋪設長為26m的籬笆圍墻,學校設計在這片空地上,利用這面圍墻和用盡已有的可制作50m長的籬笆材料,圍成一個矩形花園或圍成一個半圓花園,請回答以下問題:
(1)能否圍成面積為300m2的矩形花園?若能,請寫出其中一種設計方案,若不能,請說明理由.
(2)若圍成一個半圓花園,則該如何設計?請寫出你的設計方案.(π取3.14)
(3)圍成的各種設計中,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知直線y=kx-3與x軸交于點A(4,0),與y軸交于點C,拋物線 經過點A和點C,動點P在x軸上以每秒1個長度單位的速度由拋物線與x軸的另一個交點B向點A運動,點Q由點C沿線段CA向點A運動且速度是點P運動速度的2倍.
經過點A和點C,動點P在x軸上以每秒1個長度單位的速度由拋物線與x軸的另一個交點B向點A運動,點Q由點C沿線段CA向點A運動且速度是點P運動速度的2倍.
(1)求此拋物線的解析式和直線的解析式;
(2)如果點P和點Q同時出發,運動時間為t(秒),試問當t為何值時,以A、P、Q為頂點的三角形與△AOC相似;
(3)在直線CA上方的拋物線上是否存在一點D,使得△ACD的面積最大.若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數 .
.
(1)求拋物線頂點M的坐標;
(2)設拋物線與x軸交于A,B兩點,與y軸交于C點,求A,B,C的坐標(點A在點B的左側),并畫出函數圖象的大致示意圖;
(3)根據圖象,求不等式 的解集.
的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com