
有下列4個命題:
①方程 的根是
的根是 和
和 .
.
②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ,則CD=3.
,則CD=3.
③點P(x,y)的坐標x,y滿足x2+y2+2x﹣2y+2=0,若點P也在 的圖象上,則k=﹣1.
的圖象上,則k=﹣1.
④若實數b、c滿足1+b+c>0,1﹣b+c<0,則關于x的方程x2+bx+c=0一定有兩個不相等的實數根,且較大的實數根x0滿足﹣1<x0<1.
上述4個命題中,真命題的序號是 .
①②③④
解析試題分析:①解方程可知,方程 的根是
的根是 和
和 。此命題正確。
。此命題正確。
②∵在△ABC中,∠ACB=90°,CD⊥AB于D, AD=4,BD= ,
,
∴根據射影定理CD 2=AD×BD,解得CD=3。故此命題正確。
③∵點P(x,y)的坐標x,y滿足x2+y2+2x﹣2y+2=0,
∴(x+1)2+(y﹣1)2=0,解得:x=﹣1,y=1。∴xy=﹣1。
∵點P也在 的圖象上,∴k=﹣1。故此命題正確。
的圖象上,∴k=﹣1。故此命題正確。
④∵實數b、c滿足1+b+c>0,1﹣b+c<0,
∴y=x2+bx+c的圖象如圖所示,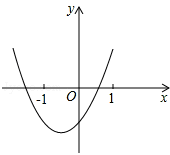
∴關于x的方程x2+bx+c=0一定有兩個不相等的實數根,且較大的實數根x0滿足﹣1<x0<1。故此選項正確。
綜上所述,真命題的序號是①②③④。


 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:填空題
如圖,是二次函數y=ax2+bx+c(a≠0)的圖象的一部分,
給出下列命題:
①abc<0;②b>2a;③a+b+c=0
④ax2+bx+c=0的兩根分別為﹣3和1;
⑤8a+c>0.其中正確的命題是 .
查看答案和解析>>
科目:初中數學 來源: 題型:計算題
某水果批發商銷售每箱進價為40元的蘋果,物價部門規定每箱售價不得高于55元,市場調查發現,若每箱以50元的價格銷售,平均每天銷售90箱,價格每提高1元,平均每天少銷售3箱.
(1)求平均每天銷售量 箱與銷售價
箱與銷售價 元/箱之間的函數關系式.
元/箱之間的函數關系式.
(2)求該批發商平均每天的銷售利潤w(元)與銷售價 (元/箱)之間的函數關系式.
(元/箱)之間的函數關系式.
(3)當每箱蘋果的銷售價為多少元時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
我市高新技術開發區的某公司,用480萬元購得某種產品的生產技術后,并進一步投入資金1520萬元購買生產設備,進行該產品的生產加工,已知生產這種產品每件還需成本費40元.經過市場調研發現:該產品的銷售單價,需定在100元到300元之間較為合理.當銷售單價定為100元時,年銷售量為20萬件;當銷售單價超過100元,但不超過200元時,每件新產品的銷售價格每增加10元,年銷售量將減少0.8萬件;當銷售單價超過200元,但不超過300元時,每件產品的銷售價格每增加10元,年銷售量將減少1萬件.設銷售單價為x(元),年銷售量為y(萬件),年獲利為w(萬元).(年獲利=年銷售額-生產成本-投資成本)
(1)直接寫出y與x之間的函數關系式;
(2)求第一年的年獲利w與x間的函數關系式,并說明投資的第一年,該公司是盈利還是虧損?若盈利,最大利潤是多少?若虧損,最少虧損是多少?
(3)若該公司希望到第二年底,除去第一年的最大盈利(或最小虧損)后,兩年的總盈利不低于1842元,請你確定此時銷售單價的范圍.在此情況下,要使產品銷售量最大,銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線y=x2+bx+c的頂點坐標為M(0,﹣1),與x軸交于A、B兩點.
(1)求拋物線的解析式;
(2)判斷△MAB的形狀,并說明理由;
(3)過原點的任意直線(不與y軸重合)交拋物線于C、D兩點,連接MC,MD,試判斷MC、MD是否垂直,并說明理由.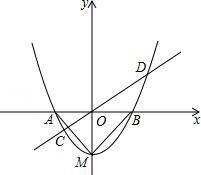
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 與x軸的交點為A、D(A在D的右側),與y軸的交點為C.
與x軸的交點為A、D(A在D的右側),與y軸的交點為C.
(1)直接寫出A、D、C三點的坐標;
(2)若點M在拋物線上,使得△MAD的面積與△CAD的面積相等,求點M的坐標;
(3)設點C關于拋物線對稱軸的對稱點為B,在拋物線上是否存在點P,使得以A、B、C、P四點為頂點的四邊形為梯形?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com