
如圖,P是邊長為1的正方形ABCD對角線AC上一動點(P與A、C不重合),點E在射線BC上,且PE=PB.設(shè)AP=x,△PBE的面積為y.則下列圖象中,能表示y與x的函數(shù)關(guān)系的圖象大致是( )
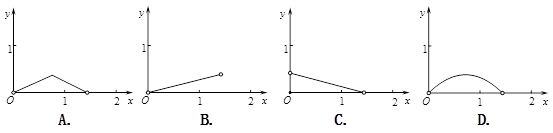
D.
解析試題分析:過點P作PF⊥BC于F,若要求△PBE的面積,則需要求出BE,PF的值,利用已知條件和正方形的性質(zhì)以及勾股定理可求出BE,PF的值.再利用三角形的面積公式得到y(tǒng)與x的關(guān)系式,此時還要考慮到自變量x的取值范圍和y的取值范圍.
過點P作PF⊥BC于F,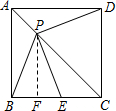
∵PE=PB,
∴BF=EF,
∵正方形ABCD的邊長是1,
∴AC=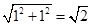 ,
,
∵AP=x,∴PC= -x,
-x,
∴PF=FC=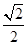 (
( -x)=1-
-x)=1-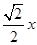 ,
,
∴BF=FE=1-FC=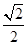 x,
x,
∴S△PBE= BE•PF=
BE•PF=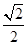 x(1-
x(1-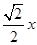 )=-
)=- x2+
x2+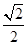 ,
,
即y=- x2+
x2+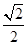 ,(0<x<
,(0<x< ),
),
∴y是x的二次函數(shù)(0<x< ),
),
故選D.
考點: 動點問題的函數(shù)圖象.


科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖是二次函數(shù)y=ax2+bx+c圖象的一部分,其對稱軸為x=-1,且過點(-3,0).下列說法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;則其中說法正確的是( ).
| A.①② | B.②③ | C.①②④ | D.②③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
對于每個x,函數(shù)y是y1=-x+6,y2=-2x2+4x+6這兩個函數(shù)的較小值,則函數(shù)y的最大值是
| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
對于拋物線y= (x+1)2+3,下列結(jié)論:①拋物線的開口向下;②對稱軸為直線x=1;③頂點坐標(biāo)為(﹣1,3);④x>﹣1時,y隨x的增大而減小,其中正確結(jié)論的個數(shù)為( )
(x+1)2+3,下列結(jié)論:①拋物線的開口向下;②對稱軸為直線x=1;③頂點坐標(biāo)為(﹣1,3);④x>﹣1時,y隨x的增大而減小,其中正確結(jié)論的個數(shù)為( )
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
拋物線y=x2-2mx+m2+m+1的頂點在( )
| A.直線y=x上 | B.直線y=x-1上 |
| C.直線x+y+1=0上 | D.直線y=x+1上 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
把二次函數(shù) 的圖象向左平移2個單位,再向上平移1個單位,所得到的圖象對應(yīng)的二次函數(shù)關(guān)系式是( )
的圖象向左平移2個單位,再向上平移1個單位,所得到的圖象對應(yīng)的二次函數(shù)關(guān)系式是( )
A. | B.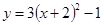 ; ; |
C.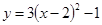 | D.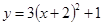 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
在平面直角坐標(biāo)系中,將函數(shù)y=2x2的圖象先向右平移1個單位,再向上平移5個單位得到圖象的函數(shù)關(guān)系式是( )
| A.y=2(x-1)2-5 | B.y=2(x-1)2+5 |
| C.y=2(x+1)2-5 | D.y=2(x+1)2+5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
西寧中心廣場有各種音樂噴泉,其中一個噴水管噴水的最大高度為3米,此時距噴水管的水平距離為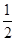 米,在如圖所示的坐標(biāo)系中,這個噴泉的函數(shù)關(guān)系式是( )
米,在如圖所示的坐標(biāo)系中,這個噴泉的函數(shù)關(guān)系式是( )
A.y=- +3 +3 | B.y=-3 +3 +3 |
C.y=-12 +3 +3 | D.y=-12 +3 +3 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com