
如圖,△ABC為等腰直角三角形,∠BAC=90°,BC=2,E為AB上任意一動點,以CE為斜邊作等腰Rt△CDE,連接AD,下列說法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四邊形ABCD的面積有最大值,且最大值為 .其中,正確的結論是 。
.其中,正確的結論是 。
| A.①②④ | B.①③⑤ | C.②③④ | D.①④⑤ |

①④⑤.
解析試題分析:首先根據已知條件看能得到哪些等量條件,然后根據得出的條件來判斷各結論是否正確.
∵△ABC、△DCE都是等腰Rt△,
∴AB=AC=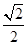 BC=
BC=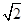 ,CD=DE=
,CD=DE=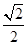 CE;
CE;
∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB-∠ACE=∠DCE-∠ACE;
即∠ECB=∠DCA;故①正確;
②當B、E重合時,A、D重合,此時DE⊥AC;
當B、E不重合時,A、D也不重合,由于∠BAC、∠EDC都是直角,則∠AFE、∠DFC必為銳角;
故②不完全正確;
④∵ ,
,
∴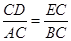 ;
;
由①知∠ECB=∠DCA,∴△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,即AD∥BC,故④正確;
③由④知:∠DAC=45°,則∠EAD=135°;
∠BEC=∠EAC+∠ECA=90°+∠ECA;
∵∠ECA<45°,∴∠BEC<135°,即∠BEC<∠EAD;
因此△EAD與△BEC不相似,故③錯誤;
⑤△ABC的面積為定值,若梯形ABCD的面積最大,則△ACD的面積最大;△ACD中,AD邊上的高為定值(即為1),若△ACD的面積最大,則AD的長最大;
由④的△BEC∽△ADC知:當AD最長時,BE也最長;
故梯形ABCD面積最大時,E、A重合,此時EC=AC=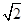 ,AD=1;
,AD=1;
故S梯形ABCD= (1+2)×1=
(1+2)×1= ,故⑤正確;
,故⑤正確;
因此本題正確的結論是①④⑤.
考點:1.相似三角形的判定;2.平行線的判定;3.等腰三角形的性質.


科目:初中數學 來源: 題型:解答題
已知,如圖,直線AB與直線BC相交于點B,點D是直線BC上一點
求作:點E,使直線DE∥AB,且點E到B、D兩點的距離相等(在題目的原圖中完成作圖)
結論:
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,在邊長為9的正方形ABCD中, F為AB上一點,連接CF.過點F作FE⊥CF,交AD于點E,若AF=3,則AE等于( ) 
| A.1 | B.1.5 | C.2 | D.2.5 |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
在比例尺是1:38000的黃浦江交通游覽圖上,某隧道長約7 ,它的實際長度約為( )
,它的實際長度約為( )
A.0.266 ; ; | B.2.66 ; ; | C.26.6 ; ; | D.266 . . |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,△ABC中,A、B兩個頂點在x軸的上方,點C的坐標是(﹣1,0).以點C為位似中心,在x軸的下方作△ABC的位似圖形△A′B′C,并把△ABC的邊長放大到原來的2倍.設點B的對應點B′的橫坐標是a,則點B的橫坐標是( )
A. B.
B. C.
C.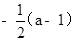 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,已知直線a∥b∥c,直線m、n與a、b、c分別交于點A、C、E、B、D、F,AC=4,CE=6,BD=3,則BF=( )
A.7 B.7.5 C.8 D.8.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com