
對于平面直角坐標系xOy中的點P(a,b),若點 的坐標為(
的坐標為( ,
,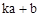 )(其中k為常數,且
)(其中k為常數,且 ),則稱點
),則稱點 為點P的“k屬派生點”.
為點P的“k屬派生點”.
例如:P(1,4)的“2屬派生點”為 (1+
(1+ ,
, ),即
),即 (3,6).
(3,6).
(1)①點P 的“2屬派生點”
的“2屬派生點”  的坐標為____________;
的坐標為____________;
②若點P的“k屬派生點”  的坐標為(3,3),請寫出一個符合條件的點P的坐標____________;
的坐標為(3,3),請寫出一個符合條件的點P的坐標____________;
(2)若點P在x軸的正半軸上,點P的“k屬派生點”為 點,且△
點,且△ 為等腰直角三角形,則k的值為____________;
為等腰直角三角形,則k的值為____________;
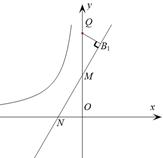
(3)如圖, 點Q的坐標為(0, ),點A在函數
),點A在函數 的圖象上,且點A是點B的“
的圖象上,且點A是點B的“ 屬派生點”,當線段B Q最短時,求B點坐標.
屬派生點”,當線段B Q最短時,求B點坐標.
(1)①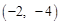 ;②(1,2)(答案不唯一);(2)
;②(1,2)(答案不唯一);(2)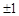 ;(3)
;(3)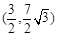 .
.
解析試題分析:(1)①根據派生點的定義,點P  的“2屬派生點”
的“2屬派生點”  的坐標為(
的坐標為(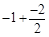 ,
,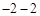 ),即
),即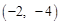 .
.
②答案不唯一,只需橫、縱坐標之和為3即可,如(1,2).
(2)若點P在x軸的正半軸上,則P(a,0),點P的“k屬派生點”為 點為(
點為(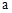 ,
,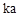 ).
).
∵且△ 為等腰直角三角形,∴
為等腰直角三角形,∴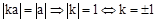 .
.
(3)求出點B所在的直線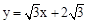 ,根據垂直線段最短的性質即可求得B點坐標.
,根據垂直線段最短的性質即可求得B點坐標.
試題解析:(1)①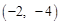 .
.
②.(1,2).
(2)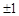 .
.
(3)設B(a,b).
∵B的“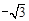 屬派生點”是A,∴
屬派生點”是A,∴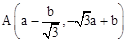 .
.
∵點A還在反比例函數 的圖象上,
的圖象上,
∴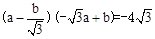 .∴
.∴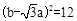 .
.
∵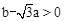 ,∴
,∴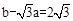 .∴
.∴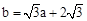 .
.
∴B在直線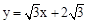 上.
上.
過Q作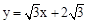 的垂線QB1,垂足為B1,
的垂線QB1,垂足為B1,
∵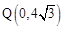 ,且線段BQ最短,∴B1即為所求的點B.
,且線段BQ最短,∴B1即為所求的點B.
∴易求得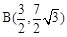 .
.
考點:1.新定義;2.開放型;3.等腰直角三角形的性質;4.曲線上點的坐標與方程的關系;5.垂直線段最短的性質.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:解答題
如圖,矩形OABC的頂點B的坐標為(1,2),反比例函數y= (0<m<2)的圖象與AB交于點E,與BC交于點F,連接OE、OF、EF.
(0<m<2)的圖象與AB交于點E,與BC交于點F,連接OE、OF、EF.
(1)若點E是AB的中點,則m= ,S△OEF= ;
(2)若S△OEF=2S△BEF,求點E的坐標;
(3)是否存在點E及y軸上的點M,使得△MFE與△BFE全等?若存在,寫出此時點E的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,點A,B分別在 軸,
軸,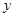 軸上,點D在第一象限內,DC⊥
軸上,點D在第一象限內,DC⊥ 軸于點C,AO=CD=2,AB=DA=
軸于點C,AO=CD=2,AB=DA= ,反比例函數
,反比例函數 的圖象過CD的中點E。
的圖象過CD的中點E。
(1)求證:△AOB≌△DCA;
(2)求 的值;
的值;
(3)△BFG和△DCA關于某點成中心對稱,其中點F在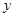 軸上,試判斷點G是否在反比例函數的圖象上,并說明理由。(
軸上,試判斷點G是否在反比例函數的圖象上,并說明理由。(
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,四邊形ABCD是平行四邊形,點A(1,0),B(3,1),C(3,3).反比例函數 的函數圖象經過點D,點P是一次函數y=kx+3-3k(k≠0)的圖象與該反比例函數圖象的一個公共點.
的函數圖象經過點D,點P是一次函數y=kx+3-3k(k≠0)的圖象與該反比例函數圖象的一個公共點.
(1)求反比例函數的解析式;
(2)通過計算,說明一次函數y=kx+3-3k(k≠0)的圖象一定過點C;
(3)對于一次函數y=kx+3-3k(k≠0),當y隨x的增大而增大時,確定點P的橫坐標的取值范圍(不必寫出過程).
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,反比例函數 的圖象和矩形ABCD在第二象限,AD平行于x軸,且AB=2,AD=4,點C的坐標為(-2,4).
的圖象和矩形ABCD在第二象限,AD平行于x軸,且AB=2,AD=4,點C的坐標為(-2,4).
(1)直接寫出A、B、D三點的坐標;
(2)若將矩形只向下平移,矩形的兩個頂點恰好同時落在反比例函數的圖象上,求反比例函數的解析式和此時直線AC的解析式y=mx+n.并直接寫出滿足 的x取值范圍.
的x取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知反比例函數y= (k為常數,k≠1).
(k為常數,k≠1).
(1)其圖象與正比例函數y=x的圖象的一個交點為P,若點P的縱坐標是2,求k的值;
(2)若在其圖象的每一支上,y隨x的增大而減小,求k的取值范圍;
(3)若其圖象的一支位于第二象限,在這一支上任取兩點 A(x1,y1)、B(x2,y2),當y1>y2時,試比較x1與x2的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com