
閱讀下面的材料:
小明遇到一個問題:如圖(1),在□ABCD中,點(diǎn)E是邊BC的中點(diǎn),點(diǎn)F是線段AE上一點(diǎn),BF的延長線交射線CD于點(diǎn)G.如果 ,求
,求 的值.
的值.

他的做法是:過點(diǎn)E作EH∥AB交BG于點(diǎn)H,則可以得到△BAF∽△HEF.
請你回答:(1)AB和EH的數(shù)量關(guān)系為???? ,CG和EH的數(shù)量關(guān)系為???? , 的值為???? .
的值為???? .
(2)如圖(2),在原題的其他條件不變的情況下,如果 ,那么
,那么 的值為???? (用含a的代數(shù)式表示).
的值為???? (用含a的代數(shù)式表示).

(3)請你參考小明的方法繼續(xù)探究:如圖(3),在四邊形ABCD中,DC∥AB,點(diǎn)E是BC延長線上一點(diǎn),AE和BD相交于點(diǎn)F. 如果 ,那么
,那么 的值為???? (用含m,n的代數(shù)式表示).
的值為???? (用含m,n的代數(shù)式表示).

(1)3,2, ;(2)
;(2) ;(3)mn.
;(3)mn.
【解析】
試題分析:(1)過E點(diǎn)作平行線,構(gòu)造相似三角形,利用相似三角形和中位線的性質(zhì),分別將各相關(guān)線段均統(tǒng)一用EH來表示,最后求得比值;
(2)先作EH∥AB交BG于點(diǎn)H,得出△EFH∽△AFB,即可得出 ,再根據(jù)AB=CD,表示出CD,根據(jù)平行線的性質(zhì)得出△BEH∽△BCG,即可表示出
,再根據(jù)AB=CD,表示出CD,根據(jù)平行線的性質(zhì)得出△BEH∽△BCG,即可表示出 ,從而得出
,從而得出 的值;
的值;
(3)先過點(diǎn)E作EH∥AB交BD的延長線于點(diǎn)H,得出EH∥AB∥CD,根據(jù)EH∥CD,得出△BCD∽△BEH,再進(jìn)一步證出△ABF∽△EHF,從而得出 的值.
的值.
試題解析:(1)過點(diǎn)E作EH∥AB交BG于點(diǎn)H,
則有△ABF∽△HEF,
∴ ,
,
∴AB=3EH.
∵平行四邊形ABCD中,EH∥AB,
∴EH∥CD,
又∵E為BC中點(diǎn),
∴EH為△BCG的中位線,
∴CG=2EH,
∴ ;
;
(2)作EH∥AB交BG于點(diǎn)H,則△EFH∽△AFB,
∴ ,
,
∴AB=aEH.
∵AB=CD,
∴CD=aEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴ ,
,
∴CG=2EH.
∴ ;
;
(3)過點(diǎn)E作EH∥AB交BD的延長線于點(diǎn)H,則有EH∥AB∥CD,
∵EH∥CD,
∴△BCD∽△BEH,
∴ ,
,
∴CD=nEH.
又 ,
,
∴AB=mCD=mnEH.
∵EH∥AB,
∴△ABF∽△EHF,
∴ .
.
考點(diǎn):相似形綜合題.


 靈星計算小達(dá)人系列答案
靈星計算小達(dá)人系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:閱讀理解
 閱讀下面的材料:
閱讀下面的材料:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:閱讀理解

查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013屆北京市西城區(qū)(北區(qū))九年級上學(xué)期期末考試數(shù)學(xué)試卷(帶解析) 題型:解答題
閱讀下面的材料:
小明在學(xué)習(xí)中遇到這樣一個問題:若1≤x≤m,求二次函數(shù) 的最大值.他畫圖研究后發(fā)現(xiàn),
的最大值.他畫圖研究后發(fā)現(xiàn), 和
和 時的函數(shù)值相等,于是他認(rèn)為需要對
時的函數(shù)值相等,于是他認(rèn)為需要對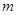 進(jìn)行分類討論.
進(jìn)行分類討論.
他的解答過程如下:
∵二次函數(shù) 的對稱軸為直線
的對稱軸為直線 ,
,
∴由對稱性可知, 和
和 時的函數(shù)值相等.
時的函數(shù)值相等.
∴若1≤m<5,則 時,
時, 的最大值為2;
的最大值為2;
若m≥5,則 時,
時, 的最大值為
的最大值為 .
.
請你參考小明的思路,解答下列問題:
(1)當(dāng) ≤x≤4時,二次函數(shù)
≤x≤4時,二次函數(shù) 的最大值為_______;
的最大值為_______;
(2)若p≤x≤2,求二次函數(shù) 的最大值;
的最大值;
(3)若t≤x≤t+2時,二次函數(shù) 的最大值為31,則
的最大值為31,則 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013-2014學(xué)年北京海淀區(qū)九年級第一學(xué)期期中測評數(shù)學(xué)試卷(解析版) 題型:解答題
閱讀下面的材料:
小明在研究中心對稱問題時發(fā)現(xiàn):
如圖1,當(dāng)點(diǎn) 為旋轉(zhuǎn)中心時,點(diǎn)
為旋轉(zhuǎn)中心時,點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),點(diǎn)
點(diǎn),點(diǎn) 再繞著點(diǎn)
再繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),這時點(diǎn)
點(diǎn),這時點(diǎn) 與點(diǎn)
與點(diǎn) 重合.
重合.
如圖2,當(dāng)點(diǎn) 、
、 為旋轉(zhuǎn)中心時,點(diǎn)
為旋轉(zhuǎn)中心時,點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),點(diǎn)
點(diǎn),點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),點(diǎn)
點(diǎn),點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),點(diǎn)
點(diǎn),點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn),小明發(fā)現(xiàn)P、
點(diǎn),小明發(fā)現(xiàn)P、 兩點(diǎn)關(guān)于點(diǎn)
兩點(diǎn)關(guān)于點(diǎn) 中心對稱.
中心對稱.



(1)請在圖2中畫出點(diǎn) 、
、 ,
小明在證明P、
,
小明在證明P、 兩點(diǎn)關(guān)于點(diǎn)
兩點(diǎn)關(guān)于點(diǎn) 中心對稱時,除了說明P、
中心對稱時,除了說明P、 、
、 三點(diǎn)共線之外,還需證明;
三點(diǎn)共線之外,還需證明;
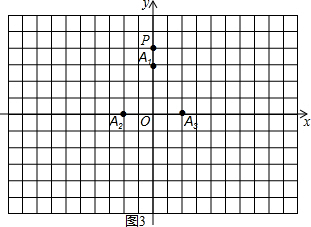
(2)如圖3,在平面直角坐標(biāo)系xOy中,當(dāng) 、
、 、
、 為旋轉(zhuǎn)中心時,點(diǎn)
為旋轉(zhuǎn)中心時,點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn);點(diǎn)
點(diǎn);點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn);點(diǎn)
點(diǎn);點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到
旋轉(zhuǎn)180°得到 點(diǎn);點(diǎn)
點(diǎn);點(diǎn) 繞著點(diǎn)
繞著點(diǎn) 旋轉(zhuǎn)180°得到點(diǎn)
旋轉(zhuǎn)180°得到點(diǎn) . 繼續(xù)如此操作若干次得到點(diǎn)
. 繼續(xù)如此操作若干次得到點(diǎn) ,則點(diǎn)
,則點(diǎn) 的坐標(biāo)為(),點(diǎn)
的坐標(biāo)為(),點(diǎn) 的坐為.
的坐為.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com