
| 打折前一次性購物總金額 | 優惠措施 |
| 不超過400元 | 售價打九折 |
| 超過400元 | 售價打八折 |
| 9 |
| 4 |
| 81-9n |
| 4 |


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 (2013•益陽)我市某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且溫度為18℃的條件下生長最快的新品種.圖是某天恒溫系統從開啟到關閉及關閉后,大棚內溫度y(℃)隨時間x(小時)變化的函數圖象,其中BC段是雙曲線y=
(2013•益陽)我市某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且溫度為18℃的條件下生長最快的新品種.圖是某天恒溫系統從開啟到關閉及關閉后,大棚內溫度y(℃)隨時間x(小時)變化的函數圖象,其中BC段是雙曲線y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
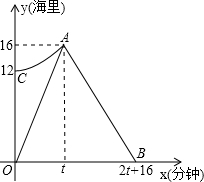 (2013•連云港)我市某海域內有一艘輪船發生故障,海事救援船接到求救信號后立即從港口出發沿直線勻速前往救援,與故障漁船會合后立即將其拖回.如圖折線段O-A-B表示救援船在整個航行過程中離港口的距離y(海里)隨航行時間x(分鐘)的變化規律.拋物線y=ax2+k表示故障漁船在漂移過程中離港口的距離y(海里)隨漂移時間x(分鐘)的變化規律.已知救援船返程速度是前往速度的
(2013•連云港)我市某海域內有一艘輪船發生故障,海事救援船接到求救信號后立即從港口出發沿直線勻速前往救援,與故障漁船會合后立即將其拖回.如圖折線段O-A-B表示救援船在整個航行過程中離港口的距離y(海里)隨航行時間x(分鐘)的變化規律.拋物線y=ax2+k表示故障漁船在漂移過程中離港口的距離y(海里)隨漂移時間x(分鐘)的變化規律.已知救援船返程速度是前往速度的| 2 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•遵義)我市某中學在創建“特色校園”的活動中,將本校的辦學理念做成宣傳牌(AB),放置在教學樓的頂部(如圖所示).小明在操場上的點D處,用1米高的測角儀CD,從點C測得宣傳牌的底部B的仰角為37°,然后向教學樓正方向走了4米到達點F處,又從點E測得宣傳牌的頂部A的仰角為45°.已知教學樓高BM=17米,且點A,B,M在同一直線上,求宣傳牌AB的高度(結果精確到0.1米,參考數據:
(2013•遵義)我市某中學在創建“特色校園”的活動中,將本校的辦學理念做成宣傳牌(AB),放置在教學樓的頂部(如圖所示).小明在操場上的點D處,用1米高的測角儀CD,從點C測得宣傳牌的底部B的仰角為37°,然后向教學樓正方向走了4米到達點F處,又從點E測得宣傳牌的頂部A的仰角為45°.已知教學樓高BM=17米,且點A,B,M在同一直線上,求宣傳牌AB的高度(結果精確到0.1米,參考數據:| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com