
(本題10分)問題情境
已知矩形的面積為a(a為常數,a>0),當該矩形的長為多少時,它的周長最小?最小值是多少?
數學模型
設該矩形的一邊長為x,周長為y,則y與x的函數關系式為 .
 探索研究
探索研究
⑴我們可以借鑒以前研究函數的經驗,先探索函數的圖象性質.
①填寫下表,畫出函數的圖象:
|
x |
…… |
|
|
|
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |

|
③在求二次函數y=ax+bx+c(a≠0)的最大(小)值時,除了通過觀察圖象,還可以通過
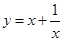
配方得到.請你通過配方求函數(x>0)的最小值.
解決問題
⑵用上述方法解決“問題情境”中的問題,直接寫出答案.
科目:初中數學 來源: 題型:
(本題10分)問題情境
已知矩形的面積為a(a為常數,a>0),當該矩形的長為多少時,它的周長最小?最小值是多少?
數學模型
設該矩形的一邊長為x,周長為y,則y與x的函數關系式為 .
![]() 探索研究
探索研究
⑴我們可以借鑒以前研究函數的經驗,先探索函數的圖象性質.
①填寫下表,畫出函數的圖象:
| x | …… |
|
|
| 1 | 2 | 3 | 4 | …… |
| y | …… |
|
|
|
|
|
|
| …… |

|
③在求二次函數y=ax+bx+c(a≠0)的最大(小)值時,除了通過觀察圖象,還可以通過
![]()
配方得到.請你通過配方求函數(x>0)的最小值.
解決問題
⑵用上述方法解決“問題情境”中的問題,直接寫出答案.
查看答案和解析>>
科目:初中數學 來源: 題型:
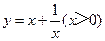
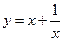
| x | …… | 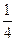 | 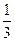 | 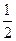 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
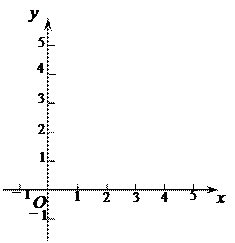
|
查看答案和解析>>
科目:初中數學 來源:2011年初中畢業升學考試(浙江金華卷)數學 題型:解答題
(本題10分)某班師生組織植樹活動,上午8時從學校出發,到植樹地點植樹后原路返校,如圖為師生離校路程s與時間t之間的圖象.請回答下列問題:
(1)求師生何時回到學校?
(2)如果運送樹苗的三輪車比師生遲半小時出發,與師生同路勻速前進,早半小時到達植樹地點,請在圖中,畫出該三輪車運送樹苗時,離校路 程s與時間t之間的圖象,并結合圖象直接寫出三輪車追上師生時,離學校的路程;
程s與時間t之間的圖象,并結合圖象直接寫出三輪車追上師生時,離學校的路程;
(3)如果師生騎自行車上午8時出發,到植樹地點后,植樹需2小時,要求14時前返回到學校,往返平均速度分別為每時10km、8km.現有A、B、C、D四個植樹點與學校的路程分別是13km、15km、17km、19km,試通過計算說明哪幾個植樹點符合要求.
查看答案和解析>>
科目:初中數學 來源:2011-2012年浙江省衢州華外九年級上學期第二次質量檢測數學卷 題型:解答題
(本題10分)問題情境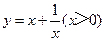

已知矩形的面積為a(a為常數,a>0),當該矩形的長為多少時,它的周長最小?最小值是多少?
數學模型
設該矩形的一邊長為x,周長為y,則y與x的函數關系式為 .
探索研究
⑴我們可以借鑒以前研究函數的經驗,先探索函數的圖象性質.
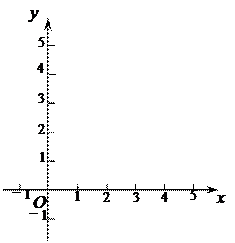
①填寫下表,畫出函數的圖象:
| x | …… |  | 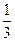 | 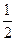 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com