
 s,則s與x的函數關系式為:s=-x2+
s,則s與x的函數關系式為:s=-x2+| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| x |
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||||
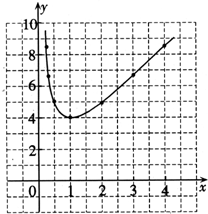
| y | … | 8
|
6
|
5 | 4 | 5 | 6
|
8
|
… |
| x |
| 1 | ||
(
|
| x |
| 1 | ||
(
|
| x |
| 1 | ||
|
| x |
| 1 | ||
|


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com