
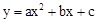 的頂點A(2,0),與y軸的交點為B(0,-1).
的頂點A(2,0),與y軸的交點為B(0,-1).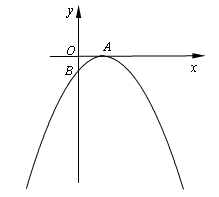
 (2)(5,
(2)(5, 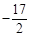 )(3)當t=5時,
)(3)當t=5時, 有最大值,最大值是
有最大值,最大值是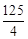
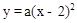 。
。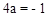 ,∴
,∴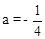 。
。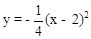 ,即
,即 。
。
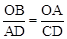 。∴OB·CD=OA·AD,即1·
。∴OB·CD=OA·AD,即1·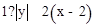 。∴
。∴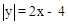 。
。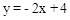 。
。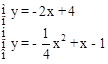 解得:
解得: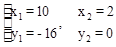 。
。 (OB+CD)=
(OB+CD)=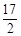 。
。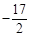 )。
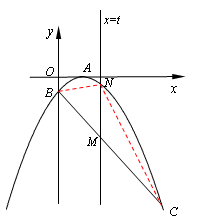
)。 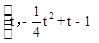 ,直線x=t(0<t<10)與直線BC交于點M,
,直線x=t(0<t<10)與直線BC交于點M,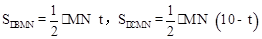 ,
,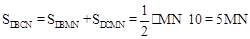 。
。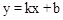 ,
,
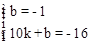 ,解得:
,解得: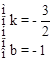 。
。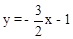 。
。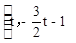 。
。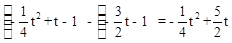 ,
,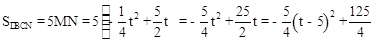 。
。 有最大值,最大值是
有最大值,最大值是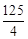 。
。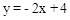 ,再根據點C在拋物線上,聯立兩個關系式組成方程組,求出x,y的值,再根據點C所在的象限確定點C的坐標。P為BC的中點,取OD中點H,連PH,則PH為梯形OBCD的中位線,可得OH=
,再根據點C在拋物線上,聯立兩個關系式組成方程組,求出x,y的值,再根據點C所在的象限確定點C的坐標。P為BC的中點,取OD中點H,連PH,則PH為梯形OBCD的中位線,可得OH=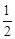 OD=5,PH=
OD=5,PH= (OB+CD)=
(OB+CD)=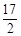 ,從而求出點P的坐標。
,從而求出點P的坐標。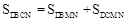 得
得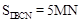 ,所以求
,所以求 的最大值就是求MN的最大值,而M,N兩點的橫坐標相同,所以MN就等于點N的縱坐標減去點M的縱坐標,從而形成關于MN長的二次函數解析式,利用二次函數的最值求解。
的最大值就是求MN的最大值,而M,N兩點的橫坐標相同,所以MN就等于點N的縱坐標減去點M的縱坐標,從而形成關于MN長的二次函數解析式,利用二次函數的最值求解。

科目:初中數學 來源:不詳 題型:解答題

 的值;
的值; 的值都等于同一個常數.
的值都等于同一個常數.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 經過點A、B、C.
經過點A、B、C.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 ),C(1,
),C(1, ),動點P從點O以每秒2個單位的速度向點A運動,動點Q也同時從點B沿B→ C→O的線路以每秒1個單位的速度向點O運動,當點P到達A點時,點Q也隨之停止,設點P、Q運動的時間為t(秒).
),動點P從點O以每秒2個單位的速度向點A運動,動點Q也同時從點B沿B→ C→O的線路以每秒1個單位的速度向點O運動,當點P到達A點時,點Q也隨之停止,設點P、Q運動的時間為t(秒).
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 銷售量】
銷售量】| 銷售單價x(元/kg) | 10 | 11 | 13 |
| 銷售量y(kg) | | | |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 0 | -3 | -4 | -3 | 0 | … |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com