
如圖,△ABC中,∠C=90°,BC=8cm, ,點P從B點出發,沿BC方向以2cm/m的速度移動,點Q從C出發,沿CA方向以1cm/m的速度移動。若P、Q同時分別從B、C出發,經過多少時間△CPQ與△CBA相似?
,點P從B點出發,沿BC方向以2cm/m的速度移動,點Q從C出發,沿CA方向以1cm/m的速度移動。若P、Q同時分別從B、C出發,經過多少時間△CPQ與△CBA相似?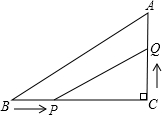
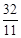 或
或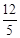 秒.
秒.
解析試題分析:根據勾股定理求得AB,AC的長,分△ABC∽△PQC和△ABC∽△QPC兩種情況討論即可.
試題解析:由5AC﹣3AB=0,得到5AC=3AB,
設AB為5xcm,則AC=3xcm,
在Rt△ABC中,由BC=8cm,根據勾股定理得:25x2=9x2+64,解得x=2.
∴AB=5x=10cm,AC=3x=6cm.
設經過t秒△ABC和△PQC相似.則有BP=2tcm,PC=(8﹣2t)cm,CQ=tcm,
分兩種情況:①當△ABC∽△PQC時,有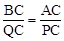 ,即
,即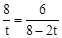 ,解得
,解得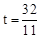 ;
;
②當△ABC∽△QPC時,有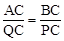 ,即
,即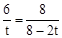 ,解得
,解得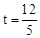 .
.
綜上可知,經過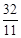 或
或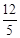 秒,△ABC和△PQC相似
秒,△ABC和△PQC相似
考點:1.雙動點問題;2.勾股定理;3.相似三角形的性質;4.分類思想的應用.


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:初中數學 來源: 題型:解答題
如圖,在邊長為1的正方形網格內有一個三角形ABC
(1)把△ABC沿著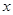 軸向右平移5個單位得到△A1B1C1,請你畫出△A1B1C1
軸向右平移5個單位得到△A1B1C1,請你畫出△A1B1C1
(2)請你以O點為位似中心在第一象限內畫出△ABC的位似圖形△A2B2C2,使得△ABC與△A2B2C2的位似比為1:2;
(3)請你寫出△A2B2C2三個頂點的坐標。(3分)
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在梯形ABCD中,AB//CD,點E在線段DA上,直線CE與BA的延長線交于點G,
(1)求證:△CDE∽△GAE;
(2)當DE:EA=1:2時,過點E作EF//CD交BC于點F且 CD=4,EF=6,求AB的長
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,點E是矩形ABCD中CD邊上一點,△BCE沿BE折疊為△BFE,點F落在AD上.
(1)求證:△ABF∽△DFE
(2)若△BEF也與△ABF相似,請求出 的值 .
的值 .
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖所示,在Rt△ABC中,AB=BC=4,∠ABC=90°,點P是△ABC的外角∠BCN的角平分線上一個動點,點P′是點P關于直線BC的對稱點,連結PP′交BC于點M,BP′交AC于D,連結BP、AP′、CP′.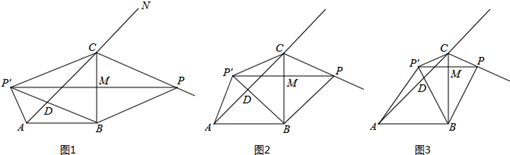
(1)若四邊形BPCP′為菱形,求BM的長;
(2)若△BMP′∽△ABC,求BM的長;
(3)若△ABD為等腰三角形,求△ABD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com