
如圖,已知矩形OABC中,OA=2,AB=4,雙曲線 (k>0)與矩形兩邊AB、BC分別交于E、F.
(k>0)與矩形兩邊AB、BC分別交于E、F.
(1)若E是AB的中點,求F點的坐標;
(2)若將△BEF沿直線EF對折,B點落在x軸上的D點,作EG⊥OC,垂足為G,請證明△EGD∽△DCF,并求出k的值.
(1)點F的坐標為(4,1);(2)證明見解析,k=3.
解析試題分析:(1)根據點E是AB中點,可求出點E的坐標,將點E的坐標代入反比例函數解析式可求出k的值,再由點F的橫坐標為4,可求出點F的縱坐標,繼而得出答案;
(2)證明∠GED=∠CDF,然后利用兩角法可判斷△EGD∽△DCF,設點E坐標為(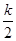 ,2),點F坐標為(4,
,2),點F坐標為(4,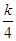 ),即可得CF=
),即可得CF=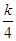 ,BF=DF=2﹣
,BF=DF=2﹣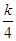 ,在Rt△CDF中表示出CD,利用對應邊成比例可求出k的值.
,在Rt△CDF中表示出CD,利用對應邊成比例可求出k的值.
試題解析:(1)∵點E是AB的中點,OA=2,AB=4,
∴點E的坐標為(2,2),
將點E的坐標代入y= ,可得k=4,
,可得k=4,
即反比例函數解析式為:y=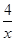 ,
,
∵點F的橫坐標為4,
∴點F的縱坐標=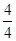 =1,
=1,
故點F的坐標為(4,1);
(2)由折疊的性質可得:BE=DE,BF=DF,∠B=∠EDF=90°,
∵∠CDF+∠EDG=90°,∠GED+∠EDG=90°,
∴∠CDF=∠GED,
又∵∠EGD=∠DCF=90°,
∴△EGD∽△DCF,
結合圖形可設點E坐標為(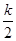 ,2),點F坐標為(4,
,2),點F坐標為(4,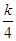 ),
),
則CF=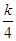 ,BF=DF=2﹣
,BF=DF=2﹣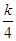 ,ED=BE=AB﹣AE=4﹣
,ED=BE=AB﹣AE=4﹣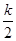 ,
,
在Rt△CDF中,CD=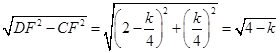 ,
,
∵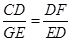 ,即
,即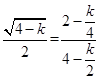 ,
,
∴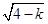 =1,
=1,
解得:k=3.
考點:反比例函數綜合題.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
如圖,將透明三角形紙片PAB的直角頂點P落在第四象限,頂點A、B分別落在反比例函數 圖象的兩支上,且PB⊥x于點C,PA⊥y于點D,AB分別與x軸,y軸相交于點E、F.已知B(1,3).
圖象的兩支上,且PB⊥x于點C,PA⊥y于點D,AB分別與x軸,y軸相交于點E、F.已知B(1,3).
(1)k= ;
(2)試說明AE=BF;
(3)當四邊形ABCD的面積為 時,求點P的坐標.
時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,矩形OABC放置在第一象限內,已知A(3,0),∠AOB=30°,反比例函數y= 的圖像交BC、AB于點D、E.
的圖像交BC、AB于點D、E.
(1)若點D為BC的中點,試證明點E為AB的中點;
(2)若點A關于直線OB的對稱點為F,試探究:點F是否落在該雙曲線上?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:如圖,正比例函數 的圖象與反比例函數
的圖象與反比例函數 的圖象交于點
的圖象交于點
(1)試確定上述正比例函數和反比例函數的表達式;
(2)根據圖象回答,在第一象限內,當 取何值時,反比例函數的值大于正比例函數的值?
取何值時,反比例函數的值大于正比例函數的值?
(3)M(m,n)是反比例函數圖像上的一動點,其中0<m<3,過M作直線MB‖x軸交y軸于點B。過點A作直線AC∥y軸交于點C,交直線MB于點D,當四邊形OADM的面積為6時,請判斷線段BM與DM的大小關系,并說明理由;
(4)探索:x軸上是否存在點P,使ΔOAP是等腰三角形?若存在,求出點P的坐標,若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
函數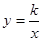 和
和 的圖象關于y軸對稱,我們定義函數
的圖象關于y軸對稱,我們定義函數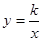 和
和 相互為“影像”函數。
相互為“影像”函數。
類似地,如果函數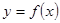 和
和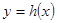 的圖象關于y軸對稱,那么我們定義函數
的圖象關于y軸對稱,那么我們定義函數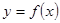 和
和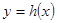 互為“影像”函數。
互為“影像”函數。
(1)請寫出函數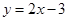 的“影像”函數: ;
的“影像”函數: ;
(2)函數 的“影像”函數是 ;
;
(3)如果,一條直線與一對“影像”函數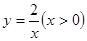 和
和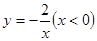 的圖象分別交于點A、B、C(點A、B在第一象限),如果CB: BA=1:2,點C在函數
的圖象分別交于點A、B、C(點A、B在第一象限),如果CB: BA=1:2,點C在函數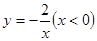 的“影像”函數上的對應點的橫坐標是1,求點B的坐標。
的“影像”函數上的對應點的橫坐標是1,求點B的坐標。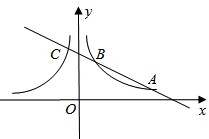
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
制作一種產品,需先將材料加熱達到60 ℃后,再進行操作.設該材料溫度為y(℃),從加熱開始計算的時間為x(min).據了解,當該材料加熱時,溫度y與時間x成一次函數關系;停止加熱進行操作時,溫度y與時間x成反比例關系(如圖).已知該材料在操作加熱前的溫度為15 ℃,加熱5分鐘后溫度達到60 ℃.
(1)分別求出將材料加熱和停止加熱進行操作時,y與x的函數關系式;
(2)根據工藝要求,當材料的溫度低于15 ℃時,須停止操作,那么從開始加熱到停止操作,共經歷了多少時間?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
一次函數 的圖像與反比例函數
的圖像與反比例函數 的圖象交于A(-2,1),B(1,n)兩點.
的圖象交于A(-2,1),B(1,n)兩點.
(1)試確定上述反比例函數和一次函數的表達式;
(2)求△OAB的面積.
(3)寫出反比例函數值大于一次函數值的自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,一次函數 (k≠0)的圖象與反比例函數
(k≠0)的圖象與反比例函數 (m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且
(m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且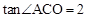 .
.
(1)求該反比例函數和一次函數的解析式;
(2)求點B的坐標;
(3)在x軸上求點E,使△ACE為直角三角形.(直接寫出點E的坐標)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com