
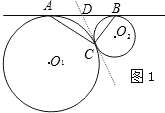
閱讀下列材料:如圖,⊙O1和⊙O2外切于點C,AB是⊙O1和⊙O2的外公切線,A、B為切點,求證:AC⊥BC.
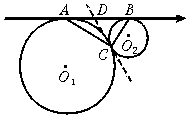
證實:過點C作⊙O1和⊙O2的內公切線交AB于D.
∵ DA、DC是⊙O1的切線,∴ DA=DC.
∴ ∠DAC=∠DCA.同理∠DCB=∠DBC.
又∵ ∠DAC+∠DCA+∠DCB+∠DBC=180°,∴ ∠DCA+∠DCB=90°.
即AC⊥BC.
根據上述材料,解答下列問題:
(1)在以上的證實過程中使用了哪些定理?請寫出兩個定理的名稱或內容;
(2)以AB所在直線為x軸,過點C且垂直于AB的直線為y軸建立直角坐標系(如圖11).已知A、B兩點的坐標為(-4,0)、(1,0),求經過A、B、C三點的拋物線y=ax2+bx+c的函數解析式;
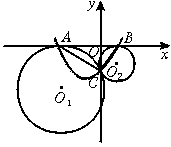
(3)根據(2)中所確定的拋物線,試判定這條拋物線的頂點是否落在兩圓的連心O1O2上,并說明理由.
解:(1)切線長定理,等腰三角形的性質定理,三角形的內角和等于180°等
(2)由題意OA=4,OB=1,AC⊥BC,Rt△ACB中,∵ AC⊥BC,CO⊥AB,∴ △BOC∽△COA.
∴ ![]() ,OC2=OA?OB,∴ OC2=4,OC=2.
,OC2=OA?OB,∴ OC2=4,OC=2.
∴ 點C(0,-2)設y=a(x+4)(x-1),代入點C(0,-2)有:-2=-4a.
∴ a= ![]() .∴ y=
.∴ y= ![]() (x+4)(x-1).即y=
(x+4)(x-1).即y= ![]() x2+
x2+ ![]() x-2.
x-2.
(3)解法一:設⊙O1的半徑為R,⊙O2的半徑為r.
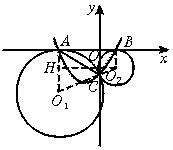
連O1A、O2B、O1O2,過O2作O2H⊥O1A于H.
在Rt△O1O2H中,O1H=R-r,O1O2=R+r,HO2=AB=5,在梯形ABO2O1中, ![]() .
.
∴ ![]()
∴ R=5,r= ![]() .
.
∴ 梯形AO1O2B的中位線長為: ![]() (R+r)=
(R+r)= ![]() (5+
(5+ ![]() )=
)= ![]() .
.
∵ 由拋物線的對稱性知,梯形中位線在對稱軸上.
∴ O1O2的中點坐標是(- ![]() ,-
,- ![]() ).
).
∵ y= ![]() (x+
(x+ ![]() )2-
)2- ![]() ,∴ 頂點P(-
,∴ 頂點P(- ![]() ,-
,- ![]() ).
).
∴ 拋物線的頂點在O1O2的連心線上.
解法二:(接解法一)由R=5,A(-4,0),C(0,-2),
∴ 點O1=(-4,-5).設過點O1、O2的直線為y=kx+b,又點C在連心線O1、O2上,
∴ ![]() ∴
∴ ![]()
∴ y= ![]() x-2.
x-2.
當x=- ![]() 時,y=
時,y= ![]() ×(-
×(- ![]() )-2=-
)-2=- ![]() .
.
∴ 頂點(- ![]() ,-
,- ![]() )在連心線O1O2上.
)在連心線O1O2上.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
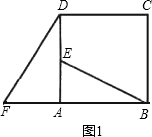
 閱讀下列材料:
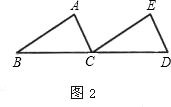
閱讀下列材料: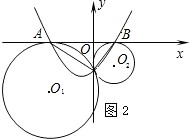
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| AM |
| MB |
| m |
| n |
| bm+an |
| m+n |

查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com