
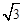 ),且在x軸上截得的線段AB的長為6.
),且在x軸上截得的線段AB的長為6.
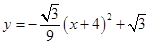 ;(2)(0,
;(2)(0,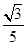 );(3)(2,
);(3)(2,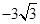 )或(-10,
)或(-10,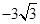 )
)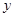 軸的對稱點
軸的對稱點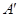 ,可得
,可得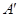 (1,0),連接
(1,0),連接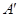 C交
C交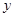 軸于一點即點M,此時MC+MA的值最小,設直線C
軸于一點即點M,此時MC+MA的值最小,設直線C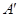 的解析式為
的解析式為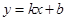 (k≠0),根據待定系數法求得函數關系式,即可得到結果;
(k≠0),根據待定系數法求得函數關系式,即可得到結果;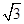 ),設對稱軸交x軸于點D,分①AB=AN1=6,②AB=BN2,③N3A=N3B,三種情況討論即可.
),設對稱軸交x軸于點D,分①AB=AN1=6,②AB=BN2,③N3A=N3B,三種情況討論即可.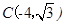 ,
, 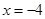 .
.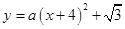
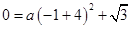
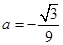
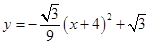 ;
;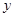 軸的對稱點
軸的對稱點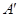 ,可得
,可得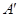 (1,0),連接
(1,0),連接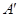 C交
C交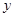 軸于一點即點M,此時MC+MA的值最小
軸于一點即點M,此時MC+MA的值最小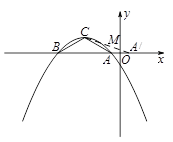
 =
= C
C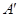 C上時,MA+MC取得最小值
C上時,MA+MC取得最小值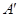 C與
C與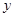 軸的交點即為所求點M
軸的交點即為所求點M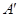 的解析式為
的解析式為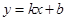 (k≠0)
(k≠0) 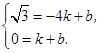
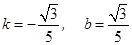
 的解析式為
的解析式為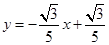
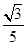 );
);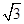 ),設對稱軸交x軸于點D
),設對稱軸交x軸于點D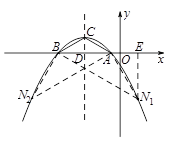
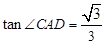
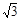 ,AE=3
,AE=3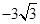 )
)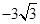 )
)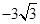 )與N2(-10,
)與N2(-10,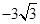 )都在拋物線上
)都在拋物線上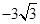 )或(-10,
)或(-10,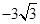 ).
).

科目:初中數學 來源:不詳 題型:解答題
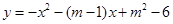 交x軸負半軸于點A,交y軸正半軸于點B(0,3),頂點C位于第二象限,連結AB,AC,BC.
交x軸負半軸于點A,交y軸正半軸于點B(0,3),頂點C位于第二象限,連結AB,AC,BC.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
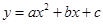 的圖象與
的圖象與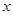 軸交于點
軸交于點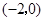 、
、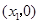 ,且
,且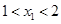 ,與
,與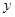 軸的正半軸的交點在
軸的正半軸的交點在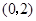 的下方.下列結論:①
的下方.下列結論:①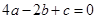 ;②
;②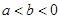 ;③
;③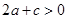 ;④
;④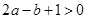 .其中正確結論的個數是 個。 ( )
.其中正確結論的個數是 個。 ( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 。
。查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 ,下列說法正確的是 ( )
,下列說法正確的是 ( )| A.當x=2時,有最大值-3; | B.當x=-2時,有最大值-3; |
| C.當x=2時,有最小值-3; | D.當x=-2時,有最小值-3; |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com