
寧波元康水果市場某批發商經銷一種高檔水果,如果每千克盈利10元,每天可售出500千克,經市場調查發現,在進貨價不變的情況下,若每千克漲價一元,日銷售量將減少20千克.
(1)現要保證每天盈利6000元,同時又要讓顧客得到實惠,那么每千克應漲價多少元?
(2)若該批發商單純從經濟角度看,那么每千克應漲價多少元,能使商場獲利最多.
(1)要保證每天盈利6000元,同時又使顧客得到實惠,那么每千克應漲價5元;
(2)若該商場單純從經濟角度看,每千克這種水果漲價7.5元,能使商場獲利最多.
解析試題分析:本題的關鍵是根據題意列出一元二次方程,再求其最值.
試題解析:(1)設每千克應漲價x元,則(10+x)(500﹣20x)="6" 000
解得x=5或x=10,
為了使顧客得到實惠,所以x=5;
(2)設漲價x元時總利潤為y,
則y=(10+x)(500﹣20x)
=﹣20x2+300x+5000
=﹣20(x2﹣15x)+5000
=﹣20(x2﹣15x+ ﹣
﹣ )+5000
)+5000
=﹣20(x﹣7.5)2+6125
當x=7.5時,y取得最大值,最大值為6 125.
答:(1)要保證每天盈利6000元,同時又使顧客得到實惠,那么每千克應漲價5元;
(2)若該商場單純從經濟角度看,每千克這種水果漲價7.5元,能使商場獲利最多.
考點:二次函數的應用.


 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:初中數學 來源: 題型:解答題
某個體戶春節前代理銷售某種品牌的酒,已知進價為每件40元,生產廠家要求銷售價不少于40元,且不大于70元,市場調查發現:若每件以50元銷售,平均每天可銷售90件,價格每降低1元,平均每天多銷售3件,價格每升高1元,平均每天少銷售3件.
(1)寫出平均每天銷售量y(件)與每件銷售價x(元)之間的函數關系式,并注明自變量的取值范圍;
(2)求出該個體戶每天銷售這種酒的毛利潤W(元)與每件酒的售價x(元)之間的函數關系式,并注明自變量的取值范圍(每件的毛利潤=售價-進價);
(3)當酒的售價為多少時平均每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 與
與 軸相交于A、B兩點,與
軸相交于A、B兩點,與 軸相交于點C,若已知B點的坐標為B(8,0).
軸相交于點C,若已知B點的坐標為B(8,0).
(1)求拋物線的解析式及其對稱軸方程;
(2)連接AC、BC,試判斷△AOC與△COB是否相似?并說明理由;
(3)M為拋物線上BC之間的一點,N為線段BC上的一點,若MN∥ 軸,求MN的最大值;
軸,求MN的最大值;
(4)在拋物線的對稱軸上是否存在點Q,使△ACQ為等腰三角形?若存在,求出符合條件的Q點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線與x軸相交于兩點A(1,0),B(-3,0),與y軸相交于點C(0,3).
(1)求此拋物線的函數表達式;
(2)如果點 是拋物線上的一點,求△ABD的面積.
是拋物線上的一點,求△ABD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
小趙投資銷售一種進價為每件20元的護眼臺燈.銷售過程中發現,當月內銷售單價不變,則月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數: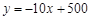 .
.
(1)設小趙每月獲得利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?并求出最大利潤.
(2)如果小趙想要每月獲得的利潤不低于2000元,那么如何制定銷售單價才可以實現這一目標?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 (b,c是常數,且c<0)與
(b,c是常數,且c<0)與 軸分別交于點A、B(點A位于點B的左側),與
軸分別交于點A、B(點A位于點B的左側),與 軸的負半軸交于點C,點A的坐標為(-1,0).
軸的負半軸交于點C,點A的坐標為(-1,0).
(1)請直接寫出點OA的長度;
(2)若常數b,c滿足關系式: .求拋物線的解析式.
.求拋物線的解析式.
(3)在(2)的條件下,點P是 軸下方拋物線上的動點,連接PB、PC.設△PBC的面積為S.
軸下方拋物線上的動點,連接PB、PC.設△PBC的面積為S.
①求S的取值范圍;
②若△PBC的面積S為整數,則這樣的△PBC共有多少個(直接寫出結果)?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 與坐標軸交于
與坐標軸交于 三點,點
三點,點 的橫坐標為
的橫坐標為 ,過點
,過點 的直線
的直線 與
與 軸交于點
軸交于點 ,點
,點 是線段
是線段 上的一個動點,
上的一個動點, 于點
于點 .若
.若 ,且
,且 .
.
(1)求 的值
的值
(2)求出點 的坐標(其中
的坐標(其中 用含
用含 的式子表示):
的式子表示):
(3)依點 的變化,是否存在
的變化,是否存在 的值,使
的值,使 為等腰三角形?
為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
天貓商城旗艦店銷售一種進價為每件20元的護眼臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數: ,在銷售過程中銷售單價不低于成本價,而每件的利潤不高于成本價的60%.
,在銷售過程中銷售單價不低于成本價,而每件的利潤不高于成本價的60%.
(1)設該旗艦店每月獲得利潤為w(元),求每月獲得利潤w(元)與銷售單價x(元)之間的函數關系式,并確定自變量x的取值范圍.
(2)當銷售單價定為多少元時,每月可獲得最大利潤?每月的最大利潤是多少?
(3)如果旗艦店想要每月獲得的利潤不低于2000元,那么每月的成本最少需要 元?
(成本=進價×銷售量)
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,正方形ABCD邊長是16 cm,P是AB上任意一點(與A、B不重合),QP⊥DP.設AP="x" cm,BQ="y" cm.試求出y與x之間的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com