中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
設0≤θ＜2π，已知兩個向量
OP1
=(cosθ，sinθ)，
OP2
=(2+sinθ，2-cosθ)，則向量
P1P2
長度的最大值是（　　）
A、
2
B、
3
C、3
2
D、2
3
分析：根據向量的減法法則求出
P1P2
的坐標，利用向量模的坐標公式和同角平方關系，化簡向量
P1P2
的模代數式，再根據已知角的范圍和余弦函數性質，求出
P1P2
模的最大值．
解答：解：由向量的減法知，
P1P2
=
OP2
-
OP1
=（2+sinθ-cosθ，2-cosθ-sinθ），
∴|
P1P2
|=
(2+sinθ-cosθ)2+(2-cosθ-sinθ)2

=
4+4(sinθ-cosθ)+(sinθ-cosθ)2+4-4(sinθ+cosθ)+(cosθ+sinθ)2

=
10-8cosθ
，
∵0≤θ＜2π，∴-1≤cosθ≤1，
則當cosθ=-1時，
P1P2
的長度有最大值是3
2
．
故選C．
點評：本題考查了向量減法和向量模的坐標運算，利用了同角的平方關系和余弦函數的性質，考查了運用知識和解決問題的能力．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設0＜θ＜
π
2
，已知a1=2cosθ，an+1=
an+2
(n∈N*)，猜想an=
 
．

查看答案和解析>>

科目：高中數學 來源： 題型：

設0＜θ＜
π
2
，已知a1=2cosθ，an+1=
2+an
（n∈N*），通過計算數列{an}的前幾項，猜想其通項公式為an=
2cos
θ
2n-1
2cos
θ
2n-1
（n∈N*）．

查看答案和解析>>

科目：高中數學 來源： 題型：

選修4-5：不等式選講
設函數f（x）=|2x+1|-|x-3|．
（1）解不等式f（x）＞0；
（2）已知關于x的不等式a+3＜f（x）恒成立，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

設0＜θ＜
π
2
，已知a1=2cosθ，an+1=
2+an
（n∈N*），猜想an等于（　　）
A、2cos
θ
2n
B、2cos
θ
2n-1
C、2cos
θ
2n+1
D、2sin
θ
2n

查看答案和解析>>

科目：高中數學 來源：2012-2013學年江蘇五校高三下學期期初教學質量調研數學卷（解析版） 題型：解答題

設非常數數列{an}滿足an+2＝，n∈N*，其中常數α，β均為非零實數，且α＋β≠0.

（1）證明：數列{an}為等差數列的充要條件是α＋2β＝0；

（2）已知α＝1，β＝， a1＝1，a2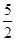＝，求證：數列{| an＋1－an－1|} (n∈N*，n≥2)與數列{n＋} (n∈N*)中沒有相同數值的項.

 

查看答案和解析>>

同步練習冊答案