已知雙曲線與橢圓
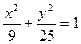
共焦點,它們的離心率之和為
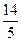
,求雙曲線方程.(10分)
雙曲線方程為:

由于橢圓焦點為F(0,

4),離心率為e=

,所以雙曲線的焦點為F(0,

4),離心率為2,
從而c=4,a=2,b=2

.
所以求雙曲線方程為:

練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若

是雙曲線
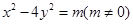
上一點,且滿足
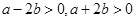
,則該點
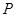
一定位于雙曲線( )
| A.右支上 | B.上支上 | C.右支上或上支上 | D.不能確定 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
一炮彈在A處的東偏北60°的某處爆炸,在A處測到爆炸信號的時間比在B處早4秒,已知A在B的正東方、相距6千米, P為爆炸地點,(該信號的傳播速度為每秒1千米)求A、P兩地的距離.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
一條漸近線方程為y=x,且過點(2,4)的雙曲線方程為__________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
雙曲線4x2-9y2=36上一點P到右焦點的距離為3,則P到左準(zhǔn)線的距離為_________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
設(shè)雙曲線與橢圓
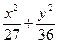
=1有共同的焦點,且與此橢圓一個交點的縱坐標(biāo)為4,求這個雙曲線的方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若k>1,則關(guān)于x、y的方程(1-k)x
2+y
2=k
2-1所表示的曲線是( )
| A.焦點在x軸上的橢圓 | B.焦點在y軸上的橢圓 |
| C.焦點在y軸上的雙曲線 | D.焦點在x軸上的雙曲線 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
P是雙曲線x2-y2=16的左支上一點,F(xiàn)1、F2分別是左、右焦點,則|PF1|-|PF2|=_________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知點M(-2,0),N(2,0),動點P滿足條件
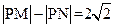
,該動點的軌跡為F,
(1)求F的方程。
(2)若A、B是F上的不同兩點,O是坐標(biāo)原點,求
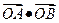
的最小值。
查看答案和解析>>

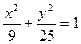 共焦點,它們的離心率之和為
共焦點,它們的離心率之和為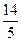 ,求雙曲線方程.(10分)
,求雙曲線方程.(10分)  一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案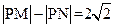 ,該動點的軌跡為F,
,該動點的軌跡為F,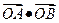 的最小值。
的最小值。