
函數(shù)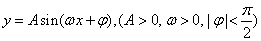 的最小值是
的最小值是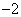 ,在一個(gè)周期內(nèi)圖象最高點(diǎn)與最低點(diǎn)橫坐標(biāo)差是
,在一個(gè)周期內(nèi)圖象最高點(diǎn)與最低點(diǎn)橫坐標(biāo)差是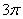 ,又:圖象過(guò)點(diǎn)
,又:圖象過(guò)點(diǎn)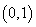 ,
,
求(1)函數(shù)解析式,
(2)函數(shù)的最大值、以及達(dá)到最大值時(shí)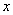 的集合;
的集合;
(3)該函數(shù)圖象可由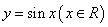 的圖象經(jīng)過(guò)怎樣的平移和伸縮得到?
的圖象經(jīng)過(guò)怎樣的平移和伸縮得到?
(4)當(dāng)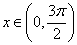 時(shí),函數(shù)的值域.
時(shí),函數(shù)的值域.
(1)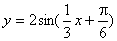 (2)2 (3)向左平移
(2)2 (3)向左平移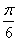 個(gè)單位,橫坐標(biāo)伸長(zhǎng)到原來(lái)的3倍,縱坐標(biāo)變?yōu)樵瓉?lái)的2倍 (4)
個(gè)單位,橫坐標(biāo)伸長(zhǎng)到原來(lái)的3倍,縱坐標(biāo)變?yōu)樵瓉?lái)的2倍 (4)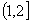
【解析】
試題分析:(1)易知:A =" 2" 半周期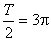 ∴T
= 6p 即
∴T
= 6p 即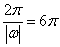 (
(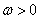 ) 從而:
) 從而: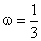 設(shè):
設(shè):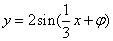 令x = 0 有
令x = 0 有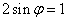 又:
又: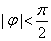 ∴
∴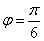
∴所求函數(shù)解析式為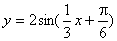 .
.
(2)令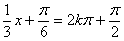 ,即
,即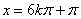 時(shí),
時(shí),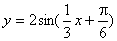 有最大值2,故當(dāng)
有最大值2,故當(dāng)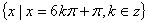 時(shí),
時(shí),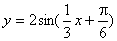 取最大值2 .
取最大值2 .
(3)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013062510595831008434/SYS201306251100403100720370_DA.files/image001.png">,所以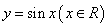 向左平移
向左平移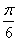 個(gè)單位得到
個(gè)單位得到 ,橫坐標(biāo)伸長(zhǎng)到原來(lái)的3倍得到
,橫坐標(biāo)伸長(zhǎng)到原來(lái)的3倍得到 ,縱坐標(biāo)伸長(zhǎng)到原來(lái)的2倍得到
,縱坐標(biāo)伸長(zhǎng)到原來(lái)的2倍得到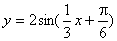 .
.
(4)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013062510595831008434/SYS201306251100403100720370_DA.files/image018.png">,所以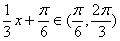 ,所以
,所以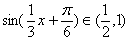 ,所以
,所以
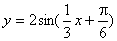
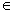
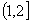 .
.
考點(diǎn):由 的部分圖象確定其解析式.
的部分圖象確定其解析式.
點(diǎn)評(píng):本題考查由 的部分圖象確定其解析式,確定A,ω,φ的值是關(guān)鍵,φ的確定是難點(diǎn),屬于中檔題.
的部分圖象確定其解析式,確定A,ω,φ的值是關(guān)鍵,φ的確定是難點(diǎn),屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| k | t |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:四川省自貢市2012屆高三第一次診斷性考試數(shù)學(xué)理科試題 題型:022
在實(shí)數(shù)集R上定義一種運(yùn)算“*”,該運(yùn)算具有性質(zhì):
①對(duì)任意a,b∈R,a*b=b*a;
②對(duì)任意a∈R,a*0=a;
③對(duì)任意a,b,c∈R,(a*b)*c=c*(ab)+(a*c)+(b*c)-2c.
則1*2=_________;函數(shù)![]() 的最小值是_________.
的最小值是_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年青海省片區(qū)高三年級(jí)大聯(lián)考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
在實(shí)數(shù)集R中定義一種運(yùn)算“﹡”,具有性質(zhì):①對(duì)任意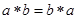 ;
;
②對(duì)任意 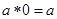 ; ③對(duì)任意
; ③對(duì)任意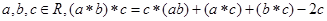
則函數(shù)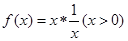 的最小值是
的最小值是
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
在實(shí)數(shù)集![]() 中定義一種運(yùn)算“
中定義一種運(yùn)算“![]() ”,具有性質(zhì):
”,具有性質(zhì):
![]() ①對(duì)任意
①對(duì)任意![]() ;
;
②對(duì)任意![]() ;
;
③對(duì)任意![]() .則
.則![]() ;函數(shù)
;函數(shù)![]() 的最小值是 .
的最小值是 .
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com