
已知向量a=
 ,b=
,b= ,c=
,c= ,
,
(1)求證:(a+b)⊥(a-b);
(2)設(shè)函數(shù)
 ,求
,求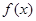 的最大值和最小值.[來
的最大值和最小值.[來
(2)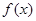 的最大值為4,最小值為0.
的最大值為4,最小值為0.
【解析】(1)計(jì)算向量的數(shù)量積;(2)將f(x)化為 4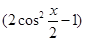 . 再由x∈
. 再由x∈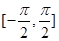 ,
得
,
得 ∈
∈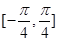 求解.
求解.
解:(1)【解法一】依題意得:a+b=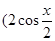 ,
,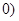 ,a-b=
,a-b=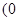 ,
,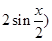
∴(a+b)·(a-b)=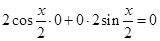 ,
,
∴(a+b)⊥(a-b). (5分)
【解法二】依題意得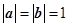 ,∴(a+b)·(a-b)=
,∴(a+b)·(a-b)=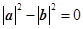 ,
,
∴(a+b)⊥(a-b). (5分)
(2)依題意得a+c=(cos +1,sin
+1,sin -1),b+c=(cos
-1),b+c=(cos +1,-sin
+1,-sin -1),
-1),
∴|a+c|2-3=(cos +1)2+(sin
+1)2+(sin -1)2-3=2cos
-1)2-3=2cos -2sin
-2sin ,
,
|b+c|2-3=(cos +1)2+(-sin
+1)2+(-sin -1)2-3=2cos
-1)2-3=2cos +2sin
+2sin ,
,
∴f(x)=(|a+c|2-3)(|b+c|2-3)=(2cos -2sin
-2sin )(2cos
)(2cos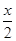 +2sin
+2sin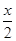 )
)
=4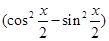 =4
=4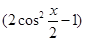 . 又x∈
. 又x∈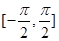 ,
∴
,
∴ ∈
∈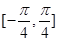
故當(dāng)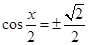 ,即
,即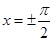 時(shí),
時(shí),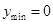 ;當(dāng)
;當(dāng) ,即
,即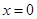 時(shí),
時(shí),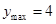
∴函數(shù)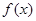 的最大值為4,最小值為0.
(12分)
的最大值為4,最小值為0.
(12分)


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:高考總復(fù)習(xí)全解 數(shù)學(xué) 一輪復(fù)習(xí)·必修課程 (人教實(shí)驗(yàn)版) B版 人教實(shí)驗(yàn)版 B版 題型:044
已知向量a=![]() ,b=
,b=![]() 且
且
x∈[0,![]() ],求:
],求:
(1)a·b及|a+b|;(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:吉林省白山二中2012屆高三第二次月考數(shù)學(xué)文科試題 題型:013
已知向量a=![]() ,b=(0,-1),c=
,b=(0,-1),c=![]() .若a-2b與c共線,則k=
.若a-2b與c共線,則k=
A.1
B.![]()
C.-1
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年上海交大附中高三數(shù)學(xué)理總復(fù)習(xí)二三角恒等變換與解三角形練習(xí)卷(解析版) 題型:選擇題
已知向量a= ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,則sin
),若a⊥b,則sin 等于( )
等于( )
A.- B.-
B.-
C. D.
D.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com