
(1)證明當x>0時,恒有f(x)>g(x);
(2)當x>0時,不等式g(x)>![]() (k≥0)恒成立,求實數k的取值范圍;
(k≥0)恒成立,求實數k的取值范圍;
(3)在x軸正半軸上有一動點D(x,0),過D作x軸的垂線依次交函數f(x)、g(x)、h(x)的圖象于點A、B、C,O為坐標原點.試將△AOB與△BOC的面積比表示為x的函數m(x),并判斷m(x)是否存在極值,若存在,求出極值;若不存在,請說明理由.
(文)已知函數f(x)=![]() ,x∈(0,+∞),數列{an}滿足a1=1,an+1=f(an);數列{bn}滿足b1=1,bn+1=
,x∈(0,+∞),數列{an}滿足a1=1,an+1=f(an);數列{bn}滿足b1=1,bn+1=![]() ,其中Sn為數列{bn}的前n項和,n=1,2,3,….
,其中Sn為數列{bn}的前n項和,n=1,2,3,….
(1)求數列{an}和數列{bn}的通項公式;
(2)設Tn=![]() ,證明Tn<3.
,證明Tn<3.
答案:(理)(1)證明:設F(x)=f(x)-g(x),則F′(x)=![]() ,
,
當x>0時,F′(x)>0,所以函數F(x)在(0,+∞)上單調遞增.又F(x)在x=0處連續,所以F(x)>F(0)=0,即f(x)-g(x)>0.所以f(x)>g(x).
(2)解:設G(x)=g(x)![]() ,則G(x)在(0,+∞)上恒大于0,G(x)=ln(1+x)-k+
,則G(x)在(0,+∞)上恒大于0,G(x)=ln(1+x)-k+![]() ,
,
G′(x)=![]() ,
,
x2+(2k-k2)x=0的根為0和k2-2k,即在區間(0,+∞)上,G′(x)=0的根為0和k2-2k,若k2-2k>0,則G(x)在(0,k2-2k)上單調遞減,且G(0)=0,與G(x)在(0,+∞)上恒大于0矛盾;若k2-2k≤0,G(x)在(0,+∞)上單調遞增,且G(0)=0,滿足題設條件,所以k2-2k≤0.所以0≤k≤2.
(3)解:m(x)= ,
,
m′(x)=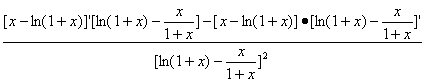 ,
,
其分母為正數,其分子為ln(1+x)·![]() .
.
由第(2)問,知ln(1+x)>![]() 在(0,+∞)上恒成立,所以m′(x)>0在(0,+∞)上恒成立,即m(x)在(0,+∞)上為單調遞增函數,故m(x)無極值.
在(0,+∞)上恒成立,所以m′(x)>0在(0,+∞)上恒成立,即m(x)在(0,+∞)上為單調遞增函數,故m(x)無極值.
(文)(1)解:∵f(x)=![]() ,an+1=f(an),∴an+1=
,an+1=f(an),∴an+1=![]() .∴
.∴![]() .
.
∴![]() 為以
為以![]() =1為首項、以2為公差的等差數列.∴
=1為首項、以2為公差的等差數列.∴![]() =1+(n-1)·2.∴an=
=1+(n-1)·2.∴an=![]() .
.
又∵f(x)=![]() ,bn+1=
,bn+1=![]() ,∴bn+1=
,∴bn+1=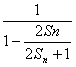 =2Sn+1.
=2Sn+1.
∴bn+2=2Sn+1+1.∴bn+2-bn+1=2(Sn+1-Sn).∴bn+2=3bn+1.∵b1=1,b2=2S1+1=3,∴{bn}為以b1=1為首項、以q=3為公比的等比數列.bn=3n-1.
(2)證明:依題意Tn=1·1+3·![]() +5·(
+5·(![]() )2+7·(
)2+7·(![]() )3+…+(2n-1)(
)3+…+(2n-1)(![]() )n-1,
)n-1,
![]() Tn=1·
Tn=1·![]() +3·(
+3·(![]() )2+5·(
)2+5·(![]() )3+…+(2n-3)·(
)3+…+(2n-3)·(![]() )n-1+(2n-1)·(
)n-1+(2n-1)·(![]() )n,
)n,
∴![]() Tn=1+2[
Tn=1+2[![]() +(
+(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n-1]-(2n-1)·(
)n-1]-(2n-1)·(![]() )n=1+2·
)n=1+2·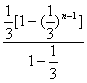 -(2n-1)(
-(2n-1)(![]() )n.
)n.
∴![]() Tn=2-(
Tn=2-(![]() )n-1-(2n-1)(
)n-1-(2n-1)(![]() )n.
)n.
∴Tn=3-![]() ·(
·(![]() )n-1-
)n-1-![]() ·(2n-1)(
·(2n-1)(![]() )n<3.
)n<3.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:高中數學 來源: 題型:

 (理)已知函數f(x)=
(理)已知函數f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中數學 來源: 題型:
| sin2x-(a-4)(sinx-cosx)+a |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•普陀區三模)(理)已知函數f(x)=
(2011•普陀區三模)(理)已知函數f(x)=| ln(2-x2) | |x+2|-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com