Question

設一直角三角形兩直角邊的長均是區間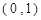的隨機數，則斜邊的長小于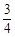的概率為   　　　　。

 

Answer 1

【答案】

【解析】

試題分析：由題意知本題是一個幾何概型，是常說的“約會”問題，解法同一般的幾何概型一樣，看出試驗包含的所有事件對應的集合，求出面積，寫出滿足條件的集合和面積，求比值即可。解：由題意知本題是一個幾何概型，∵兩直角邊都是0，1間的隨機數，設兩直角邊分別是x，y．∴試驗包含的所有事件是{x，y|0＜x＜1，0＜y＜1}，對應的正方形的面積是1，滿足條件的事件對應的集合{（x，y）|x²+y²＜9/16，x＞0，y＞0．}，這個圖形是一個1/4圓，面積是，題目即求它與邊長為1的正方行面積的比P=，故答案為

考點：幾何概型

點評：古典概型和幾何概型是我們學習的兩大概型，古典概型要求能夠列舉出所有事件和發生事件的個數，而不能列舉的就是幾何概型，幾何概型的概率的值是通過長度、面積、和體積、的比值得到．