Question

 

設是定義在區間上的函數，其導函數為。如果存在實數和函數，其中對任意的都有>0，使得，則稱函數具有性質。

(1)設函數，其中為實數。

(i)求證：函數具有性質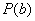； (ii)求函數的單調區間。

(2)已知函數具有性質。給定設為實數，

，，且，

若||<||，求的取值范圍。

 

數學Ⅱ（附加題）

 

Answer 1

【答案】

 [解析] 本小題主要考查函數的概念、性質、圖象及導數等基礎知識，考查靈活運用數形結合、分類討論的思想方法進行探索、分析與解決問題的綜合能力。滿分16分。

（1）(i)

∵時，恒成立，

∴函數具有性質；

(ii)（方法一）設，與的符號相同。

當時，，，故此時在區間上遞增；

當時，對于，有，所以此時在區間上遞增；

當時，圖像開口向上，對稱軸，而，

對于，總有，，故此時在區間上遞增；

（方法二）當時，對于，

   所以，故此時在區間上遞增；

當時，圖像開口向上，對稱軸，方程的兩根為：，而

 當時，，，故此時在區間     上遞減；同理得：在區間上遞增。

綜上所述，當時，在區間上遞增；

          當時，在上遞減；在上遞增。

(2)（方法一）由題意，得：

又對任意的都有>0，

所以對任意的都有，在上遞增。

又。

當時，，且，

         

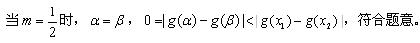
綜合以上討論，得：所求的取值范圍是（0，1）。

（方法二）由題設知，的導函數，其中函數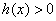對于任意的都成立。所以，當時，，從而在區間上單調遞增。

①當時，有，

，得，同理可得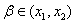，所以由的單調性知、，

從而有||<||，符合題設。

②當時，，

，于是由及的單調性知，所以||≥||，與題設不符。

③當時，同理可得，進而得||≥||，與題設不符。

因此綜合①、②、③得所求的的取值范圍是（0，1）。