
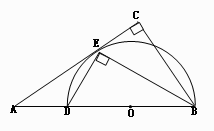
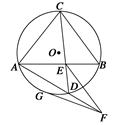
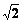 ,求BC的長。
,求BC的長。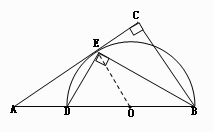
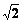 )2=6•AB,AB=12,∴OE=OD=3,AO=9
)2=6•AB,AB=12,∴OE=OD=3,AO=9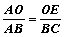 ,即
,即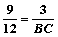 ,∴BC=4………12分
,∴BC=4………12分

 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
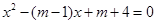 的兩根,
的兩根,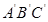 與△ABC開始時完全重合,然后讓△ABC固定不動,將
與△ABC開始時完全重合,然后讓△ABC固定不動,將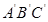 以1厘米/秒的速度沿BC所在的直線向左移動.
以1厘米/秒的速度沿BC所在的直線向左移動.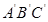 與△ABC 的重疊部分的面積為y平方厘米,求y與x之間的函數關系式,并寫出x的取值范圍;
與△ABC 的重疊部分的面積為y平方厘米,求y與x之間的函數關系式,并寫出x的取值范圍;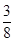 平方厘米?
平方厘米?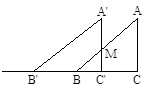
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com