
已知橢圓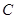 :
: =1(a>b>0)與雙曲線
=1(a>b>0)與雙曲線 有公共焦點,且離心率為
有公共焦點,且離心率為 .
.  分別是橢圓
分別是橢圓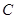 的左、右頂點. 點
的左、右頂點. 點 是橢圓
是橢圓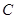 上位于
上位于 軸上方的動點.直線
軸上方的動點.直線 分別與直線
分別與直線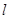 :
: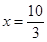 交于
交于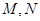 兩點.
兩點.
(I)求橢圓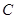 的方程;
的方程;
(II)當線段 的長度最小時,在橢圓
的長度最小時,在橢圓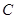 上是否存在點
上是否存在點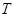 ,使得
,使得 的面積為
的面積為 ?若存在,求出
?若存在,求出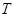 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.

解:(I)由已知得橢圓 的焦點為
的焦點為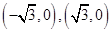 ,
,
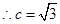 ,又
,又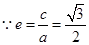 ,
,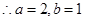 ,橢圓的方程為
,橢圓的方程為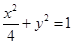 . ……..(4分)
. ……..(4分)
(II)直線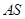 的斜率
的斜率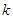 顯然存在,且
顯然存在,且 ,故可設直線
,故可設直線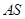 的方程為
的方程為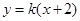 ,從而
,從而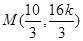 ……..(5分)
……..(5分)
由 得
得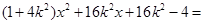 0
0
設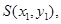 則
則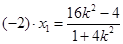 得
得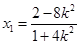 從而
從而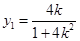
即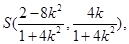 所以
所以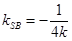
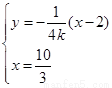 得
得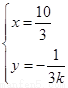
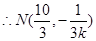 …….
……..(7分)
…….
……..(7分)
故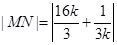 又
又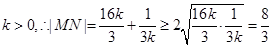
當且僅當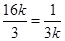 ,即
,即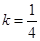 時等號成立
時等號成立
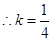 時,線段
時,線段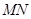 的長度取最小值
的長度取最小值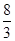 .
……..(9分)
.
……..(9分)
此時 的方程為
的方程為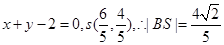
要使橢圓 上存在點
上存在點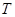 ,使得
,使得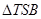 的面積等于
的面積等于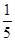 ,只須
,只須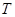 到直線
到直線 的距離等于
的距離等于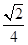 ,所以
,所以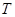 在平行于
在平行于 且與
且與 距離等于
距離等于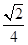 的直線
的直線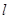 上.設直線
上.設直線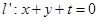
則由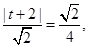 解得
解得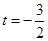 或
或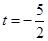
①當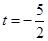 時由
時由 得
得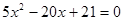 ,由于
,由于 故直線
故直線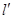 與橢圓沒有交點.
與橢圓沒有交點.
②當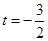 時,由
時,由 ,得
,得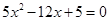
由于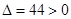 ,故直線
,故直線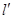 與橢圓
與橢圓 有兩個不同的交點
有兩個不同的交點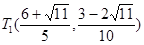 或
或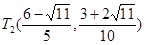 ;
;
綜上所述,當線段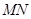 的長度最小時,在橢圓
的長度最小時,在橢圓 上僅存在兩個不同的點
上僅存在兩個不同的點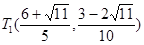 或
或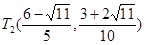 ,使得
,使得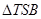 的面積為
的面積為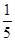 .
……………..(12分)
.
……………..(12分)
【解析】略


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源:2010-2011學年湖北省天門市高三模擬考試(一)文科數學 題型:選擇題
已知橢圓 +
+ =1(a>b>0)與雙曲線
=1(a>b>0)與雙曲線 -
- =1有相同的焦點,則橢圓的離心率為
=1有相同的焦點,則橢圓的離心率為
A. B.
B. C.
C. D.
D.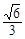
查看答案和解析>>
科目:高中數學 來源:2013屆湖南省華容縣高二第一學期期末考試理科數學試卷 題型:解答題
(本小題滿分13分)已知橢圓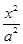 +
+ =1(a>b>0)上的點M(1,
=1(a>b>0)上的點M(1,
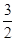 )到它的兩焦點F1,F2的距離之和為4,A、B分別是它的左頂點和上頂點。
)到它的兩焦點F1,F2的距離之和為4,A、B分別是它的左頂點和上頂點。
(1)求此橢圓的方程及離心率;
(2)平行于AB的直線l與橢圓相交于P、Q兩點,求|PQ|的最大值及此時直線l的方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com