Question

（08年湖南卷理）（本小題滿分13分）

若A、B是拋物線上的不同兩點，弦AB（不平行于y軸）的垂直平分線與

x軸相交于點P，則稱弦AB是點P的一條“相關弦”.已知當時，點

存在無窮多條“相關弦”.給定.

（I）證明：點的所有“相關弦”的中點的橫坐標相同；

(II) 試問：點的“相關弦”的弦長中是否存在最大值？

若存在，求其最大值（用x₀表示）：若不存在，請說明理由.

Answer 1

解: （I）設AB為點的任意一條“相關弦”，且點A、B的坐標分別是

,則,

兩式相減得.因為x₁x₂,所以y₁+y₂0.

設直線AB的斜率是k，弦AB的中點是,則

k=.從而AB的垂直平分線l的方程為

又點P（x₀,0）在直線上，所以

而于是故點P（x₀,0）的所有“相關弦”的中點的橫坐標都是x₀-2.

(Ⅱ)由(Ⅰ)知，弦AB所在直線的方程是，代入中，

整理得     （?）

則是方程（?）的兩個實根，且

設點P的“相關弦”AB的弦長為l，則

   

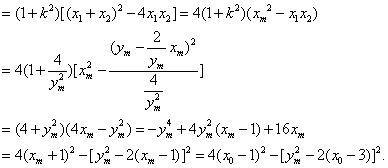
因為,于是設t=,則t(0,4x₀-8).

記^.

若,則,所以當,即=2(x₀-3)時,

l有最大值.

若,則,在區間上是減函數，

所以,l不存在最大值.

綜上所述，當x₀>3時，點的“相關弦”的弦長中存在最大值，且最大值

為2（x₀-1）；當2< x₀3時，點的“相關弦”的弦長中不存在最大值.