
����С�}�M��13�֣���֪�E�A��������ԭ�c�����c��y�S�ϣ��x���ʞ�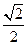 ����
����
�E�A��(j��ng)�^�A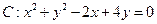 �ĈA��C��
�ĈA��C��
��I����E�A�Ę˜ʷ��̣�
��II���O(sh��)ֱ��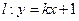 �c�E�A����A��B���c���c
�c�E�A����A��B���c���c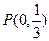 ��|PA|=|PB|����ֱ��
��|PA|=|PB|����ֱ��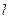 �ķ��̡�
�ķ��̡�
��1���ɈAC�ķ��̿�֪���A��C��1��-2�� ��������2��
�O(sh��)�E�A�ķ��̞�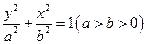
�E�A�^�A��C���ɵã�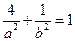
��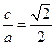 ����
����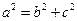 ��
��
��ã�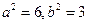
���E�A�ķ��̞飺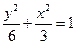 ��������6��
��������6��
��2����ֱ�������c�E�A����(li��n)�����̽M��Ԫ�ɵã�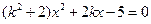
�O(sh��)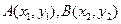
��һ���O(sh��)AB���cM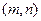
����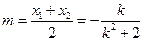 ��
�� ��������8��
��������8��
��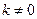 ���t��
���t�У�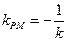 ����ã�
����ã�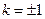 ��������10��
��������10��
��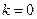 ���@Ȼ�M���}�⡣
���@Ȼ�M���}�⡣
��ֱ��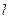 �ķ��̞飺
�ķ��̞飺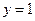 ��
��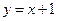 ��
�� 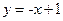 ��������13��
��������13��
��������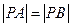 ,����ɵ÷��̣��ɽ��
,����ɵ÷��̣��ɽ��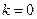 ��
��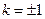
����



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�AC��������ԭ�c�����c��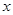 �S�ϣ��ԃɂ����c�Ͷ��S�ăɂ����c����c����߅����һ����e��8�������Σ�ӛ��Q��.
�S�ϣ��ԃɂ����c�Ͷ��S�ăɂ����c����c����߅����һ����e��8�������Σ�ӛ��Q��.
������E�AC�ķ���;
�����O(sh��)�cP�ǙE�AC����ʾ��c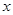 �S�Ľ��c���^�cP��ֱ��
�S�Ľ��c���^�cP��ֱ��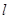 �c�E�AC�ཻ��M,N���c��������MN�����c����������Q��(n��i)������߅�磩�r����ֱ��
�c�E�AC�ཻ��M,N���c��������MN�����c����������Q��(n��i)������߅�磩�r����ֱ��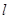 ��б�ʵ�ȡֵ������
��б�ʵ�ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��14�֣�
�E�A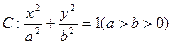 �^�cP
�^�cP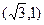 �����x���ʞ�
�����x���ʞ�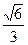 ��F(xi��n)��E�A���ҽ��c��
��F(xi��n)��E�A���ҽ��c��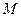 ��
��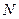 ���c�ڙE�A
���c�ڙE�A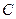 �ϣ���
�ϣ��� 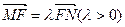 �����c
�����c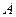 ����4��0����
����4��0����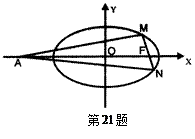
������E�AC�ķ��̣�
����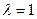 �r ������MN�cAF�Ƿ�ֱ�����C����ĽY(ji��)Փ.
�r ������MN�cAF�Ƿ�ֱ�����C����ĽY(ji��)Փ.
����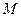 ��
��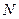 ���c��
���c��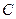 ���\�ӣ���
���\�ӣ���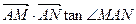 =6
=6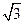 �r
�r , ��ֱ��MN�ķ���.
, ��ֱ��MN�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�����}11�֣���D1�����タy=ax2��bx��c(a��0)����c�飨1,4������x�S��A��B����y�S��D������B�c�����˞飨3,0��
��1�����タ�Ľ���ʽ
��2����D 2���^�cA��ֱ���c���タ�����cE����y�S���cF������E�c�ęM���˞�2����ֱ��PQ�钁�タ�Č��Q�S���cG��PQ��һ���c���t
2���^�cA��ֱ���c���タ�����cE����y�S���cF������E�c�ęM���˞�2����ֱ��PQ�钁�タ�Č��Q�S���cG��PQ��һ���c���t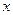 �S���Ƿ����һ�cH��ʹD��G��F��H���c���ɵ���߅�����L��С.�����ڣ�����@����Сֵ��G��H����
�S���Ƿ����һ�cH��ʹD��G��F��H���c���ɵ���߅�����L��С.�����ڣ�����@����Сֵ��G��H���� �ˣ��������ڣ�Ո�f������.
�ˣ��������ڣ�Ո�f������.
��3����D3�����タ���Ƿ����һ�c ���^�c
���^�c ��
��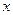 �S�Ĵ����������
�S�Ĵ���������� ���^�c
���^�c ��ֱ��
��ֱ�� ��������
��������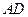 ���c
���c ���B��
���B�� ��ʹ
��ʹ ��
��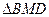 �������ڣ�����c
�������ڣ�����c �����ˣ��������ڣ��f������.
�����ˣ��������ڣ��f������.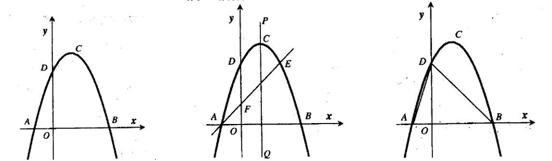 �D1 �D2
�D1 �D2  �D3
�D3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(12��) ��D��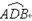 ���A��AB���Aֱ����O���A�A�ģ���OD��AB��Q�龀��OD�����c����֪|AB|=4������C�^Q�c�����cP������C���\���ұ���|PA|+|PB|��ֵ��׃.
���A��AB���Aֱ����O���A�A�ģ���OD��AB��Q�龀��OD�����c����֪|AB|=4������C�^Q�c�����cP������C���\���ұ���|PA|+|PB|��ֵ��׃.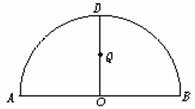
(1)�����m��?sh��)�ƽ��ֱ������ϵ��������C�ķ��̣�
(2)�^D�c��ֱ�� l�c����C�ཻ�ڲ�ͬ�ă��cM��N����M��D��N֮�g���O(sh��)
l�c����C�ཻ�ڲ�ͬ�ă��cM��N����M��D��N֮�g���O(sh��)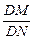 =�ˣ���˵�ȡֵ����.
=�ˣ���˵�ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A �����タ
�����タ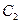 �Ľ��c����
�Ľ��c���� �S�ϣ�
�S�ϣ� �����ĺ�
�����ĺ�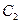 ����c����ԭ�c
����c����ԭ�c ����ÿ�l������ȡ�ɂ��c����������ӛ����±��У�
����ÿ�l������ȡ�ɂ��c����������ӛ����±��У�
 | 3 |  2 2 | 4 |  |
 |  | 0 |  4 4 |  |
 �Ę˜ʷ��̣�
�Ę˜ʷ��̣� �M��l�������^
�M��l�������^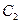 �Ľ��c
�Ľ��c �����c
�����c ����ͬ���c
����ͬ���c �ҝM��
�ҝM��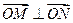 �������ڣ����ֱ��
�������ڣ����ֱ�� �ķ��̣��������ڣ��f�����ɣ�
�ķ��̣��������ڣ��f�����ɣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ����x�}
�ژO����ϵ�У��A�ѣ���2sin �ȵĈA�ĵĘO������(����)
A��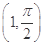 | B��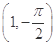 | C��(1,0) | D��(1����) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ����x�}
�ژO����ϵ�У��A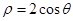 �Ĵ�ֱ�ژO�S�ăɗl�о����̷քe��(����)
�Ĵ�ֱ�ژO�S�ăɗl�о����̷քe��(����)
A��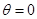 ( (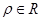 )�� )��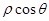 ��2 ��2 |
B��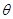 �� ��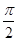 ( (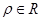 )�� )��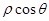 ��2 ��2 |
C��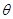 �� ��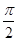 ( (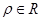 )�� )��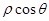 ��1 ��1 |
D��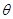 ��0( ��0(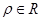 )�� )��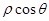 ��1 ��1 |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com