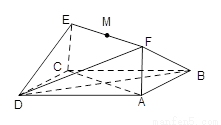
中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

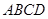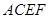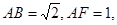
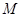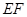如圖所示，已知正方形和矩形所在的平面互相垂直, 是線段的中點。

（1）證明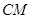：∥平面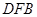

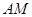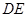（2）求異面直線與所成的角的余弦值。

 

【答案】

（1）建立空間直角坐標(biāo)系，用坐標(biāo)表示點與向量，證明CM與平面BDF的法向量垂直，即可證得結(jié)論；

（2）

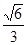
【解析】

試題分析：（1）證明：建立如圖所示的空間直角坐標(biāo)系，則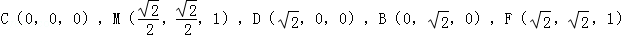…（2分）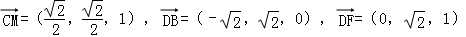

設(shè)平面DBF的一個法向量為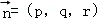，則，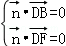

∴

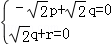
取，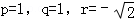

得平面DBF的一個法向量為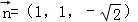，…（6分）

因為，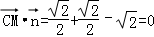

所以，

又因為直線CM?平面DBF內(nèi)，所以CM∥平面BDF．…（6分）

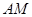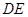（2）結(jié)合上一問可知求異面直線與所成的角的余弦值，只要確定出向量AM和向量DE的坐標(biāo)即可，結(jié)合平面向量的夾角公式來得到為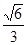

考點：線面平行，異面直線的角

點評：本題考查線面平行，考查面面角，解題的關(guān)鍵是建立空間直角坐標(biāo)系，用坐標(biāo)表示點與向量，利用向量的數(shù)量積求解

 

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：

如圖所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
2
，AF=1，M是線段EF的中點．
（1）證明：CM∥平面DFB
（2）求異面直線AM與DE所成的角的余弦值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

（2011•廣州模擬）如圖所示，已知正方形ABCD的邊長為2，AC∩BD=O．將正方形ABCD沿對角BD折起，得到三棱錐A-BCD．
（1）求證：平面AOC⊥平面BCD；
（2）若三棱錐A-BCD的體積為
6
3
，求AC的長．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

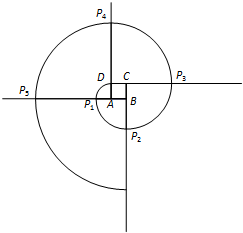（2011•豐臺區(qū)二模）如圖所示，已知正方形ABCD的邊長為1，以A為圓心，AD長為半徑畫弧，交BA的延長線于P1，然后以B為圓心，BP1長為半徑畫弧，交CB的延長線于P2，再以C為圓心，CP2長為半徑畫弧，交DC的延長線于P3，再以D為圓心，DP3長為半徑畫弧，交AD的延長線于P4，再以A為圓心，AP4長為半徑畫弧，…，如此繼續(xù)下去，畫出的第8道弧的半徑是
8
8
，畫出第n道弧時，這n道弧的弧長之和為
n(n+1)π
4
n(n+1)π
4
．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

如圖所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=，AF=1，M是線段EF的中點.

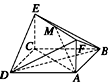
求證：

（1）AM∥平面BDE；

（2）AM⊥平面BDF.

查看答案和解析>>

同步練習(xí)冊答案