
(本小題滿分13分)
如圖,四邊形 為矩形,
為矩形, 平面
平面 ,
, 為
為 上的點,且
上的點,且 平面
平面 .
.
(1)求證: ;
;
(2)求三棱錐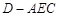 的體積;
的體積;
(3)設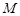 在線段
在線段 上,且滿足
上,且滿足 ,試在線段
,試在線段 上確定一點
上確定一點 ,使得
,使得 平面
平面 .
.
(1)根據線面垂直的性質定理來證明線線垂直,同時能根據∴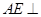 平面
平面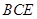 ,得到結論是關鍵的一步。
,得到結論是關鍵的一步。
(2)
(3) 點為線段
點為線段 上靠近
上靠近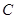 點的一個三等分點
點的一個三等分點
解析試題分析:
證明:(1)∵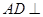 平面
平面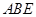 ,且
,且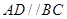
∴ 平面
平面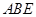 ,則
,則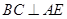 .………………………………………2分
.………………………………………2分
又∵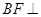 平面
平面 ,則
,則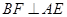 ,且
,且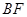 與
與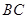 交于
交于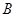 點,
點,
∴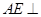 平面
平面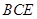 ,又
,又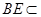 平面
平面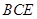 ∴
∴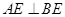 .………………4分
.………………4分
(2)由第(1)問得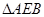 為等腰直角三角形,易求得
為等腰直角三角形,易求得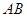 邊上的高為
邊上的高為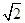 ,
,
∴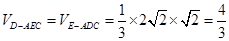 .…………………………………………………7分
.…………………………………………………7分
(3)在三角形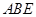 中過
中過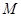 點作
點作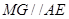 交
交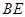 于
于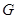 點,在三角形
點,在三角形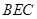 中過
中過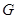 點作
點作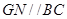 交
交 于
于 點,連
點,連 .
.
由比例關系易得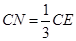 .………………………………………………………………9分
.………………………………………………………………9分
∵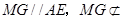 平面
平面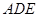 ,
,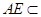 平面
平面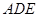 ,
,
∴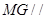 平面
平面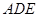 . 同理,
. 同理,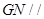 平面
平面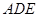 ,且
,且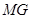 與
與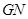 交于
交于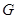 點,
點,
∴平面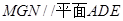 .………………………………………………………………11分
.………………………………………………………………11分
又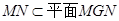 , ∴
, ∴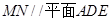 .
.
∴ 點為線段
點為線段 上靠近
上靠近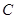 點的一個三等分點.…………………………………………13分
點的一個三等分點.…………………………………………13分
考點:線線的垂直證明,以及體積計算。
點評:解決該試題的關鍵是能利用線面垂直的性質定理來靈活的證明線線垂直,同時能根據等體積法求解體積,是常用的求解方法,屬于基礎題。


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,在三棱錐D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC的中點,F在棱AC上,且AF=3FC.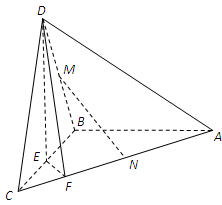
(1)求三棱錐D-ABC的表面積;
(2)求證AC⊥平面DEF;
(3)若M為BD的中點,問AC上是否存在一點N,使MN∥平面DEF?若存在,說明點N的位置;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個多面體的直觀圖和三視圖如圖所示,其中 、
、 分別是
分別是 、
、 的中點,
的中點, 是
是 上的一動點,主視圖與俯視圖都為正方形。
上的一動點,主視圖與俯視圖都為正方形。

⑴求證: ;
;
⑵當 時,在棱
時,在棱 上確定一點
上確定一點 ,使得
,使得 ∥平面
∥平面 ,并給出證明。
,并給出證明。
⑶求二面角 的平面角余弦值。
的平面角余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
如圖1,在等腰梯形 中,
中, ,
, ,
, ,
, 為
為 上一點,
上一點,  ,且
,且 .將梯形
.將梯形 沿
沿 折成直二面角
折成直二面角 ,如圖2所示.
,如圖2所示.
(Ⅰ)求證:平面 平面
平面 ;
;
(Ⅱ)設點 關于點
關于點 的對稱點為
的對稱點為 ,點
,點 在
在 所在平面內,且直線
所在平面內,且直線 與平面
與平面 所成的角為
所成的角為 ,試求出點
,試求出點 到點
到點 的最短距離.
的最短距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com