
觀察下表:
1,
2,3,
4,5,6,7![]() ,
,
8,9,10,11,12,13,14,15,
……
問:(1)此表第n行的第一個數與最后一個數分別是多少?
(2)此表第n行的各個數之和是多少?
(3)2 012是第幾行的第幾個數?
(1)此表第n行的第1![]() 個數為2n-1,第n行共有2n-1個數,依次構成公差為1的等差數列.
個數為2n-1,第n行共有2n-1個數,依次構成公差為1的等差數列.
由等差數列的通項公式,此表第n行的最后一個數是2n-1+(2n-1-1)×1=2n-1;
(2)由等差數列的求和公式,此表第n行的各個數之和為![]() =22n-2+22n-3-2n-2,或2n-1×2n-1+
=22n-2+22n-3-2n-2,或2n-1×2n-1+![]() ×1=22n-2+22n-3-2n-2.
×1=22n-2+22n-3-2n-2.
(3)設2 012在此數表的第n行.
則2n-1≤2 012≤2n-1,n∈N+,可得n=11.
故2 012在此數表的第11行.
設2 012在此數表的第11行的第m個數,而第11行的第1個數為210,
因此,2 012是第11行的第989個數.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源:2013屆福建泉州一中高二下學期期中考試文科數學試卷(解析版) 題型:填空題
觀察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
......
則第______行的各數之和等于 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖南省四市九校高三上學期12月月考文科數學 題型:填空題
觀察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
………………………………………………
則第
行的各數之和等于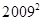
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省棗莊市高三上學期期末檢測理科數學 題型:解答題
.(本題滿分12分)
觀察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
……
問:(1)此表第n行的第一個數與最后一個數分別是多少?
(2)此表第n行的各個數之和是多少?
(3)2012是第幾行的第幾個數?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com