
在平面直角坐標系 中,已知圓
中,已知圓 的圓心為
的圓心為 ,過點
,過點 且斜率為
且斜率為 的直線與圓
的直線與圓 相交于不同的兩點
相交于不同的兩點 .
.
(Ⅰ)求 的取值范圍;
的取值范圍;
(Ⅱ)以OA,OB為鄰邊作平行四邊形OADB,是否存在常數 ,使得直線OD與PQ平行?如果存在,求
,使得直線OD與PQ平行?如果存在,求 值;如果不存在,請說明理由.
值;如果不存在,請說明理由.
(Ⅰ)先設出直線的方程,由直線與圓有兩個不同的交戰,故聯立圓方程可得得一元二次方程,由判別式大于0可得K的取值范圍為 ;(Ⅱ)沒有符合題意的常數
;(Ⅱ)沒有符合題意的常數 ,理由見解析.
,理由見解析.
解析試題分析:(Ⅰ) ;(Ⅱ)由向量加減法,可利用向量處理,設
;(Ⅱ)由向量加減法,可利用向量處理,設 ,則
,則 ,由
,由 與
與 共線等價于
共線等價于 ,然后由根與系數關系可得
,然后由根與系數關系可得 ,由(Ⅰ)知
,由(Ⅰ)知 ,故沒有符合題意的常數
,故沒有符合題意的常數 .注意運用向量法和方程的思想.
.注意運用向量法和方程的思想.
試題解析:(Ⅰ)圓的方程可寫成 ,所以圓心為
,所以圓心為 ,
,
過 且斜率為
且斜率為 的直線方程為
的直線方程為 .
.
代入圓方程得 ,整理得
,整理得 . ①
. ①
直線與圓交于兩個不同的點 等價于
等價于 ,
,
解得 ,即
,即 的取值范圍為
的取值范圍為 .
.
(Ⅱ)設 ,則
,則 ,
,
由方程①, ②
②
又 . ③
. ③
而 .
.
所以 與
與 共線等價于
共線等價于 ,
,
將②③代入上式,解得
由(Ⅰ)知 ,故沒有符合題意的常數
,故沒有符合題意的常數 .
.
考點:1.直線與圓的位置關系;2.一元二次方程的根的判別式;3.向量共線的充要條件.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:解答題
在平面直角坐標系xOy中,已知圓 :
: 和圓
和圓 :
:

(1)若直線l過點A(4,0),且被圓C1截得的弦長為2 ,求直線l的方程;
,求直線l的方程;
(2)設P為平面上的點,滿足:存在過點P的無窮多對互相垂直的直線 和
和 ,它們分別與圓
,它們分別與圓 和圓
和圓 相交,且直線
相交,且直線 被圓
被圓 截得的弦長與直線
截得的弦長與直線 被圓
被圓 截得的弦長相等,試求所有滿足條件的點P的坐標.
截得的弦長相等,試求所有滿足條件的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,已知以點 為圓心的圓與直線
為圓心的圓與直線 相切,過點
相切,過點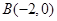 的動直線
的動直線 與圓
與圓 相交于
相交于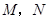 兩點,
兩點, 是
是 的中點,直線
的中點,直線 與
與 相交于點
相交于點 .
.
(1)求圓 的方程;
的方程;
(2)當 時,求直線
時,求直線 的方程;
的方程;
(3) 是否為定值?如果是,求出其定值;如果不是,請說明理由.
是否為定值?如果是,求出其定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在平面直角坐標系 中,點
中,點 ,直線
,直線 ,設圓
,設圓 的半徑為,圓心在上.
的半徑為,圓心在上.
(1)若圓心 也在直線
也在直線 上,過點
上,過點 作圓
作圓 的切線,求切線的方程;
的切線,求切線的方程;
(2)若圓 上存在點
上存在點 ,使
,使 ,求圓心
,求圓心 的橫坐標
的橫坐標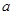 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
己知圓C: (x – 2 )2 + y 2 =" 9," 直線l:x + y = 0.
(1) 求與圓C相切, 且與直線l平行的直線m的方程;
(2) 若直線n與圓C有公共點,且與直線l垂直,求直線n在y軸上的截距b的取值范圍;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com