證明不等式
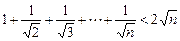
(
n∈N
*)
證法一: (1)當
n等于1時,不等式左端等于1,右端等于2,所以不等式成立:
(2)假設
n=
k(
k≥1)時,不等式成立,即1+
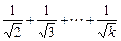
<2
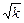
,
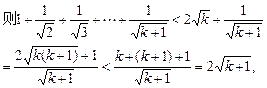
∴當
n=
k+1時,不等式成立.
綜合(1)、(2)得:當
n∈N
*時,都有1+
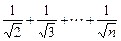
<2
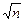
.
另從
k到
k+1時的證明還有下列證法:
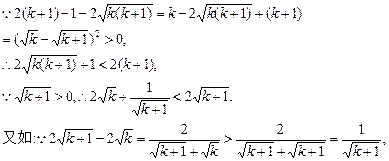
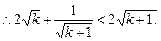
證法二: 對任意
k∈N
*,都有:
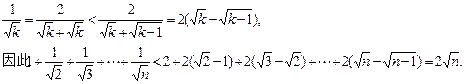
證法三:設
f(
n)=
那么對任意
k∈N
*都有:
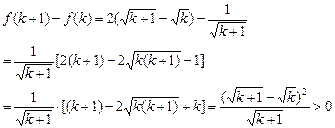
∴
f(
k+1)>
f(
k)
因此,對任意
n∈N
*都有
f(
n)>
f(
n-1)>…>
f(1)=1>0,
∴
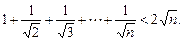
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
由下列不等式:
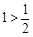
,
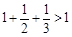
,
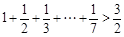
,
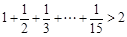
,
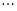
,你能得到一個怎樣的一般不等式?并加以證明.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知f(x)=
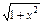
,a≠b,
求證:|f(a)-f(b)|<|a-b|.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
i,
m、
n是正整數(shù),且1<
i≤
m<
n.
(1)證明:
niA
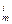
<
miA
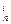

(2)證明: (1+
m)
n>(1+
n)
m
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設x1、x2、y1、y2是實數(shù),且滿足x12+x22≤1,
證明不等式(x1y1+x2y2-1)2≥(x12+x22-1)(y12+y22-1).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(1)解不等式
≥3;
(2)a,b∈R
+,2c>a+b,求證
c-<a<c+.
查看答案和解析>>

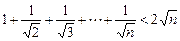 (n∈N*)
(n∈N*)