
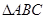 的三邊長
的三邊長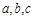 ,滿足
,滿足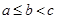
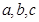 均為正整數,且
均為正整數,且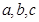 成等差數列,將滿足條件的三角形的面積從小到大排成一列
成等差數列,將滿足條件的三角形的面積從小到大排成一列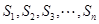 ,且
,且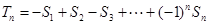 ,求滿足不等式
,求滿足不等式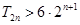 的所有
的所有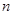 的值;
的值;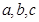 成等比數列,若數列
成等比數列,若數列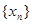 滿足
滿足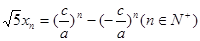 ,證明數列
,證明數列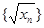 中的任意連續三項為邊長均可以構成直角三角形,且
中的任意連續三項為邊長均可以構成直角三角形,且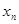 是正整數.
是正整數.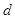 .改成
.改成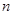 沒關系.由于數列
沒關系.由于數列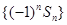 的前
的前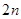 項的和的特點是每項是一項正一項負.所以相鄰的兩項用平方差公式化簡.即可得一個等差數列的求和的式子. 由
項的和的特點是每項是一項正一項負.所以相鄰的兩項用平方差公式化簡.即可得一個等差數列的求和的式子. 由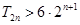 得
得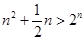 ,由于指數函數是爆炸性的變化,所以要符合該不等式的不是很多,再由
,由于指數函數是爆炸性的變化,所以要符合該不等式的不是很多,再由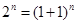 .利用二項式定理展開即可得
.利用二項式定理展開即可得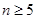 時,
時,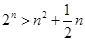 .所以
.所以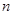 只有2,3,4三種情況.
只有2,3,4三種情況.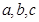 成等比數列.解直角三角形三邊的關系可求得
成等比數列.解直角三角形三邊的關系可求得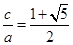 .所以可以寫出
.所以可以寫出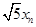 的表達式.在遞推一個式子.兩式相加,再利用
的表達式.在遞推一個式子.兩式相加,再利用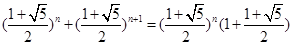 =
=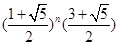 =
=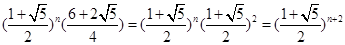 .從而可得
.從而可得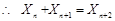 .從而即可得解答結論.再說明前三項符合即可.
.從而即可得解答結論.再說明前三項符合即可.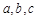 的公差為
的公差為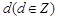 ,則
,則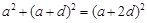
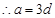
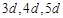 ,面積
,面積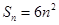 , 2分
, 2分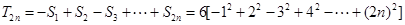
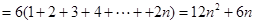
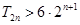 得
得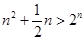 ,
,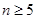 時,
時,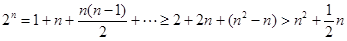 ,
, 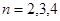 時,
時,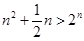 ,當
,當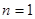 時,
時,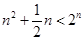
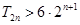 的所有
的所有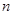 的值為2、3、4 6分
的值為2、3、4 6分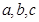 成等比數列,
成等比數列,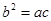 .
.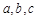 為直角三角形的三邊長,知
為直角三角形的三邊長,知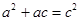 ,
,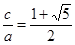 , 8分
, 8分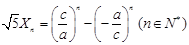 ,得
,得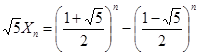 ,
,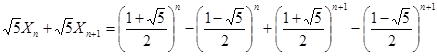
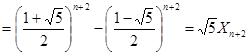
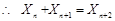 ,則有
,則有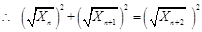 .
.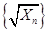 中的任意連續三項為邊長均可以構成直角三角形 10分
中的任意連續三項為邊長均可以構成直角三角形 10分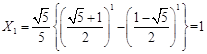 ,
,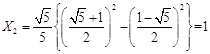
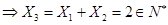 ,由數學歸納法得:
,由數學歸納法得: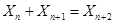 ,同理可得
,同理可得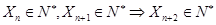 ,
,  都有
都有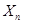 是正整數 12分
是正整數 12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com