為迎接夏季旅游旺季的到來,少林寺單獨設置了一個專門安排游客住宿的客棧,寺廟的工作人員發現為游客準備的一些食物有些月份剩余不少,浪費很嚴重,為了控制經營成本,減少浪費,就想適時調整投入.為此他們統計每個月人住的游客人數,發現每年各個月份來客棧人住的游客人數會發生周期性的變化,并且有以下規律:
①每年相同的月份,人住客棧的游客人數基本相同;
②人住客棧的游客人數在2月份最少,在8月份最多,相差約400人;
③2月份人住客棧的游客約為100人,隨后逐月遞增直到8月份達到最多.
(1)試用一個正弦型三角函數描述一年中入住客棧的游客人數與月份之間的關系;
(2)請問哪幾個月份要準備400份以上的食物?
【答案】
分析:(1)根據①,可知函數的周期是12;根據②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400;根據③可知,f(x)在[2,8]上單調遞增,且f(2)=100,由此可得函數解析式;
(2)由條件知,200sin(
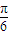
x
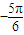
)+300≥400,結合x∈N
*,1≤x≤12,即可得到結論.
解答:解:(1)設該函數為f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π)
根據①,可知函數的周期是12,∴
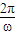
=12,∴ω=
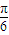
;
根據②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故該函數的振幅為200;
根據③可知,f(x)在[2,8]上單調遞增,且f(2)=100,∴f(8)=500
∴
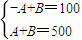
,∴
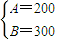
∵f(2)最小,f(8)最大,
∴sin(2×
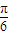
+φ)=-1,sin(8×
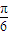
+φ)=1,
∵0<|φ|<π,
∴φ=
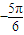
∴f(x)=200sin(
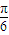
x
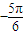
)+300;
(2)由條件知,200sin(
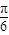
x
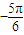
)+300≥400,化簡可得sin(
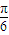
x
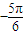
)
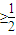
,
∴2kπ+
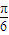
≤
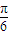
x
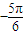
≤2kπ+
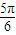
,k∈Z
∴12k+6≤x≤12k+10,k∈Z
∵x∈N
*,1≤x≤12
∴x=6,7,8,9,10
∴只有6,7,8,9,10五個月份要準備400份以上的食物.
點評:本題主要考查了在實際問題中建立三角函數模型的問題.解題的技巧是從問題中發現周期變化的規律,并將所發現的規律抽象為恰當的三角函數模型.

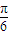 x
x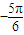 )+300≥400,結合x∈N*,1≤x≤12,即可得到結論.
)+300≥400,結合x∈N*,1≤x≤12,即可得到結論.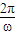 =12,∴ω=
=12,∴ω=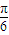 ;
;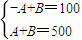 ,∴
,∴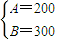
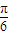 +φ)=-1,sin(8×
+φ)=-1,sin(8×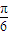 +φ)=1,
+φ)=1,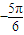
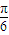 x
x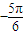 )+300;
)+300;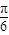 x
x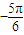 )+300≥400,化簡可得sin(
)+300≥400,化簡可得sin(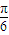 x
x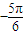 )
)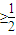 ,
,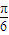 ≤
≤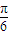 x
x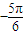 ≤2kπ+
≤2kπ+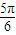 ,k∈Z
,k∈Z
