
是否存在常數 ,使等式
,使等式 對于一切
對于一切 都成立?若不存在,說明理由;若存在,請用數學歸納法證明?
都成立?若不存在,說明理由;若存在,請用數學歸納法證明?
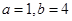 ,證明詳見解析.
,證明詳見解析.
解析試題分析:先從特殊情形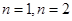 ,等式必須成立,求出
,等式必須成立,求出 值,然后用數學歸納法加以證明,在這里必須指出的是:若題目沒有講要用數學歸納法證明,我們也應從數學歸納法考慮,因為等式的左邊我們無法通過數列求和的知識解決,其次本題是與自然數有關的命題證明,我們應優先考慮數學歸納法,證明時必須嚴格遵循數學歸納法的證題步驟,做到規范化.
值,然后用數學歸納法加以證明,在這里必須指出的是:若題目沒有講要用數學歸納法證明,我們也應從數學歸納法考慮,因為等式的左邊我們無法通過數列求和的知識解決,其次本題是與自然數有關的命題證明,我們應優先考慮數學歸納法,證明時必須嚴格遵循數學歸納法的證題步驟,做到規范化.
試題解析:若存在常數 使等式成立,則將
使等式成立,則將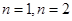 代入上式,有
代入上式,有 得
得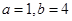 ,即有
,即有 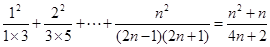 對于一切
對于一切 成立. 5分
成立. 5分
數學歸納法證明如下:
證明如下:(1)當 時,左邊=
時,左邊=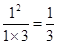 ,右邊=
,右邊= ,所以等式成立,
,所以等式成立,
(2)假設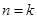 (
( 且
且 )時等式成立,即
)時等式成立,即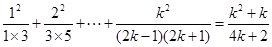 ,
,
當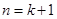 時,
時,

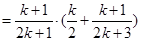
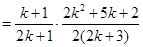


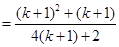
也就是說,當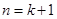 時,等式成立,
時,等式成立,
綜上所述,可知等式對任何 都成立. 12分
都成立. 12分
考點:數學歸納法.


科目:高中數學 來源: 題型:填空題
將側棱相互垂直的三棱錐稱為“直角三棱錐”,三棱錐
的側面和底面分別叫直角三棱錐的“直角面和斜面”;過三棱錐頂點及斜面任兩邊中點的截面均稱為斜面的“中面”.已知直角三角形具有性質:“斜邊的中線長等于斜邊邊長的一半”.仿照此性質寫出直角三棱錐具有的性質: .
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)已知a>b>c,且a+b+c=0,用分析法求證:<a.
(2)f(x)=,先分別求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后歸納猜想一般性結論,并給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某少數民族的刺繡有著悠久的歷史,如圖(1)、(2)、(3)、(4)為她們刺繡最簡單的四個圖案,這些圖案都是由小正方形構成,小正方形數越多刺繡越漂亮.現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含f(n)個小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“歸納推理思想”,歸納出f(n+1)與f(n)之間的關系式,并根據你得到的關系式求出f(n)的表達式;
(3)求 +
+ +
+ +…+
+…+ 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
對于命題:如果 是線段
是線段 上一點,則
上一點,則 ;將它類比到平面的情形是:若
;將它類比到平面的情形是:若 是△
是△ 內一點,有
內一點,有 ;將它類比到空間的情形應該是:若
;將它類比到空間的情形應該是:若 是四面體
是四面體 內一點,則有__________________________.
內一點,則有__________________________.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
下面給出了關于復數的三種類比推理:
(1)復數的加減法運算法則可以類比多項式的加減法運算法則;
(2)由向量 的性質
的性質 =
= 類比得到復數
類比得到復數 的性質
的性質 ;
;
(3)由向量加法的幾何意義可以類比得到復數的加法的幾何意義。
其中類比錯誤的是___________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com