【答案】
分析:(I)根據b
k為a
1,a
2…a
k中的最大值,稱數列{b
n}為{a
n}的“創新數列”,可得數列3,4,1,5,2與數列3,4,2,5,1的“創新數列”為3,4,4,5,5;
(II)設數列{c
n}的創新數列為{e
n}(n=1,2,3…,m),{e
n}為等差數列,設其公差為d,討論d=0,d=1,以及當d=2時,因為e
m=e
1+(m-1)d=2m-2+e
1,又m>3,e
1>0,所以e
m>m,這與e
m=m矛盾,所以此時{e
n}不存在,即不存在{c
n}使得它的創新數列為d=2的等差數列,從而得到結論;
(Ⅲ)由(Ⅱ)知,e
m=m,由題意,得e
1=c
1,所以當數列{c
n}的創新階數為2時,{e
n}必然為c
1,c
1,…c
1,m,m…m(其中c
1<m)由排列組合知識,得創新數列為k,k,…,k,m,m…,m的符合條件的{c
n}的個數,在創新階數為2的所有數列{c
n}中,它們的首項的和為
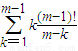
=(m-1)!
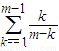
.
解答:(Ⅰ)解:由題意,創新數列為3,4,4,5,5的數列{c
n}有兩個,即:
(1)數列3,4,1,5,2;---------------------------(2分)
(2)數列3,4,2,5,1.---------------------------(3分)
注:寫出一個得(2分),兩個寫全得(3分).
(Ⅱ)答:存在數列{c
n},它的創新數列為等差數列.
解:設數列{c
n}的創新數列為{e
n}(n=1,2,3…,m),
因為e
m為c
1,c
2,…c
m中的最大值.
所以e
m=m.
由題意知:e
k為c
1,c
2,…c
k中最大值,e
k+1為c
1,c
2,…c
k+1中最大值,
若{e
n}為等差數列,設其公差為d,則d,e
k+1,e
k,0,-----------(5分)
當d=0時,{e
n}為常數列,又e
m=m,
所以數列{e
n}為m,m,m,…,m,此時數列{c
n}是首項為m的任意一個符合條件的數列;
當d=1時,因為e
m=m,
所以數列{e
n}為1,2,3…,m,此時數列{c
n}是1,2,3…,m;-----------(7分)
當d=2時,因為e
m=e
1+(m-1)d=2m-2+e
1,
又m>3,e
1>0,所以e
m>m,
這與e
m=m矛盾,所以此時{e
n}不存在,即不存在{c
n}使得它的創新數列為d=2的等差數列.
綜上,當數列{c
n}為:(1)首項為m的任意符合條件的數列;
(2)數列1,2,3…,m時,它的創新數列為等差數列.---------------------------(9分)
注:此問僅寫出結論(1)(2)者得(2分).
(Ⅲ)解:設{c
n}的創新數列為{e
n}(n=1,2,3…,m),
由(Ⅱ)知,e
m=m,
由題意,得e
1=c
1,
所以當數列{c
n}的創新階數為2時,{e
n}必然為c
1,c
1,…c
1,m,m…m(其中c
1<m),---------------------(10分)
由排列組合知識,得創新數列為k,k,…,k,m,m…,m的符合條件的{c
n}的個數為
C
m-1m-kA
m-k-1m-k-1A
k-1k-1=
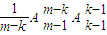
=

,----------------(12分)
所以,在創新階數為2的所有數列{c
n}中,它們的首項的和為
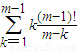
=(m-1)!
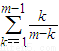
.---------------------------(14分)
點評:本題主要考查了創新數列的定義,以及分類討論的思想和排列組合等知識,對于學生有很大的難度,屬于難題.

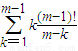 =(m-1)!
=(m-1)!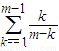 .
.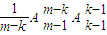 =
= ,----------------(12分)
,----------------(12分)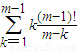 =(m-1)!
=(m-1)!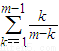 .---------------------------(14分)
.---------------------------(14分)

 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案