
(本小題滿分13分)
某種產品的廣告費支出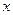 與銷售額
與銷售額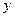 (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
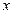 | 2 | 4 | 5 | 6 | 8 |
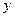 | 30 | 40 | 60 | 50 | 70 |
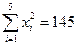
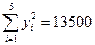
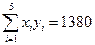 ,
,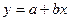 ,其中
,其中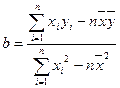 )
) 科目:高中數學 來源: 題型:解答題
(本小題滿分12分)為了了解某年段1000名學生的百米成績情況,隨機抽取了若干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.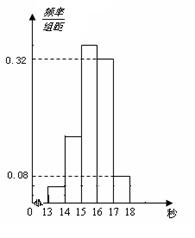
⑴將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
⑵求調查中隨機抽取了多少個學生的百米成績;
⑶若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩位學生參加數學競賽培訓.現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次.記錄如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)畫出甲、乙兩位學生成績的莖葉圖,指出學生乙成績的中位數;
(2)現要從中選派一人參加數學競賽,從平均狀況和方差的角度考慮,你認為派哪位學生參加合適?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)為了了解某年段1000名學生的百米成績情況,隨機抽取了若
干學生的百米成績,成績全部介于13秒與18秒之間,將成績按如下方式分成五組:第一組
[13,14);第二組[14,15);……;第五組[17,18].按上述分組方法得到的頻率分布直方圖如
圖所示,已知圖中從左到右的前3個組的頻率之比為3∶8∶19,且第二組的頻數為8.
(1)將頻率當作概率,請估計該年段學生中百米成績在[16,17)內的人數;
(2)求調查中隨機抽取了多少個學生的百米成績;
(3)若從第一、五組中隨機取出兩個成績,求這兩個成績的差的絕對值大于1秒的概率.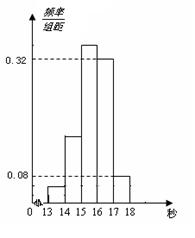
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
假設關于某設備的使用年限x和所支出的維修費用y(萬元),有如下表的統計資料:
若由資料可知y對x呈線性相關關系,試求:
(1)線性回歸直線方程;
(2)估計使用年限為.10年時,維修費用是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差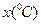 | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數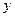 個 個 | 22 | 25 | 29 | 26 | 16 | 12 |
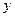 關于
關于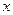 的線性回歸方程
的線性回歸方程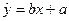 ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
本小題滿分12分)
為調查某市學生百米運動成績,從該市學生中按照男女生比例隨機抽取50名學生進行百米測試,學生成績全部都介于13秒到18秒之間,將測試結果按如下方式分成五組,第一組 ,第二組
,第二組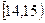 ……第五組
……第五組 ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.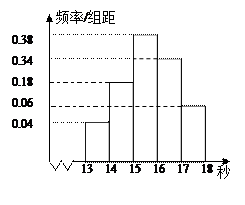
(Ⅰ)求這組數據的眾數和中位數(精確到0.1);
(II)設 表示樣本中兩個學生的百米測
表示樣本中兩個學生的百米測
試成績,已知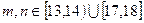
求事件“ ”的概率.
”的概率.
(Ⅲ) 根據有關規定,成績小于16秒為達標.
如果男女生使用相同的達標標準,則男女生達標情況如下 表
表
| 性別 是否達標 | 男 | 女 | 合計 |
| 達標 | 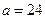 | 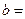 ______ ______ | _____ |
| 不達標 | 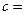 _____ _____ | 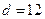 | _____ |
| 合計 | ______ | ______ | 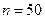 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
17.有甲乙兩個班級進行數學考 試,按照大于等于85分為優秀,85分以下為非優秀統計成績后,得到如下的列聯表:
試,按照大于等于85分為優秀,85分以下為非優秀統計成績后,得到如下的列聯表:
| | 優秀 | 非優秀 | 總計 |
| 甲班 | 10[來源:學科網ZXXK] | | |
| 乙班 | | 30 | [來源:學#科#網] |
| 合計 | | | 105 |
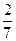
 績與班級有關系”。
績與班級有關系”。查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知x與y之間的一組數據
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
 x與y線性相關,寫出線性回歸方程必定經過的點
x與y線性相關,寫出線性回歸方程必定經過的點 =0.74
=0.74 說明什么問題。
說明什么問題。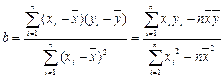
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com