
設函數 ;
;
(Ⅰ)求證:函數 在
在 上單調遞增;
上單調遞增;
(Ⅱ)設 ,若直線PQ∥x軸,求P,Q兩點間的最短距離.
,若直線PQ∥x軸,求P,Q兩點間的最短距離.
 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
已知函數 ,其中
,其中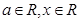 .
.
(1)當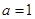 時,求函數
時,求函數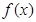 在
在 處的切線方程;
處的切線方程;
(2)若函數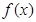 在區間(1,2)上不是單調函數,試求
在區間(1,2)上不是單調函數,試求 的取值范圍;
的取值范圍;
(3)已知 ,如果存在
,如果存在 ,使得函數
,使得函數
 在
在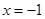 處取得最小值,試求
處取得最小值,試求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 .
.
(Ⅰ)若 在x=
在x= 處的切線與直線4x+y=0平行,求a的值;
處的切線與直線4x+y=0平行,求a的值;
(Ⅱ)討論函數 的單調區間;
的單調區間;
(Ⅲ)若函數 的圖象與x軸交于A,B兩點,線段AB中點的橫坐標為
的圖象與x軸交于A,B兩點,線段AB中點的橫坐標為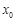 ,證明
,證明 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,現要在邊長為 的正方形
的正方形 內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為
內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為 (
( 不小于
不小于 )的扇形花壇,以正方形的中心為圓心建一個半徑為
)的扇形花壇,以正方形的中心為圓心建一個半徑為 的圓形草地.為了保證道路暢通,島口寬不小于
的圓形草地.為了保證道路暢通,島口寬不小于 ,繞島行駛的路寬均不小于
,繞島行駛的路寬均不小于 .
.
(1)求 的取值范圍;(運算中
的取值范圍;(運算中 取
取 )
)
(2)若中間草地的造價為 元
元 ,四個花壇的造價為
,四個花壇的造價為 元
元 ,其余區域的造價為
,其余區域的造價為 元
元 ,當
,當 取何值時,可使“環島”的整體造價最低?
取何值時,可使“環島”的整體造價最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com