
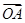 =(1,7),
=(1,7), =(5,1),
=(5,1),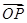 =(2,1),點Q為直線OP上一動點.
=(2,1),點Q為直線OP上一動點.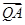 ·
· 取得最小值時,求
取得最小值時,求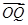 坐標;
坐標;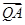 ·
· 有最小值-8,此時
有最小值-8,此時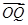 =(4,2).(2)-
=(4,2).(2)-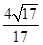 .
.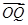 =(x,y),∴點Q在直線
=(x,y),∴點Q在直線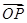 上,
上,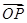 與
與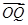 共線,又
共線,又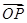 =(2,1),
=(2,1),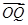 =(2y,y),
=(2y,y),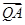 =
=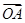 -
-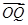 =(1-2y,7-y),
=(1-2y,7-y),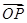 =(5-2y,1-y)
=(5-2y,1-y)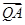 ·
· =(1-2y)·(5-2y)+(7-y)·(1-y)=5y2-20y+12=5(y-2)2-8,
=(1-2y)·(5-2y)+(7-y)·(1-y)=5y2-20y+12=5(y-2)2-8,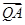 ·
· 有最小值-8,此時
有最小值-8,此時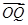 =(4,2).
=(4,2).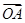 =(-3,5),
=(-3,5), =(1,-1),
=(1,-1),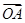 ·
·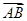 =-8,|
=-8,|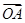 |=
|=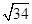 ,
,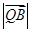 =
=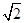 .
.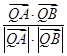 =-
=-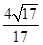 .
.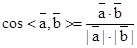 。平面向量模的計算,往往“化模為方”,轉化成向量的運算。
。平面向量模的計算,往往“化模為方”,轉化成向量的運算。

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com