
設 (
(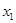 ,
,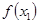 ),
), (
( ,
,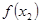 )是函數
)是函數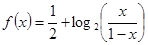 的圖象上的任意兩點.
的圖象上的任意兩點.
(1)當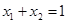 時,求
時,求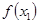 +
+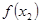 的值;
的值;
(2)設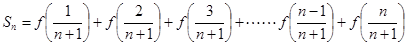 ,其中
,其中 ,求
,求
(3)對應(2)中 ,已知
,已知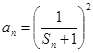 ,其中
,其中 ,設
,設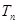 為數列
為數列 的前
的前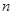 項和,求證
項和,求證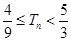 .
.
(1)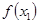 +
+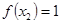 ;(2)
;(2)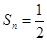 ;(3)
;(3)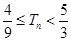
解析試題分析:(1)熟練地運用對數的三個運算性質并配以代數式的恒等變換是對數的計算、化簡、證明的常用技巧;(2)若前后項的和相加為定值,則采用倒序相加法求數列的和,其基本思想和等差數列的前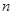 項和相類似;(3)觀測數列的特點形式,看使用什么方法求和.使用裂項法求和時,要注意正負項相消時消去了哪些項,保留了哪些項,切不可漏寫未被消去的項,未被消去的項有前后對稱的特點,實質上造成正負相消是此法的根源和目的;(4)不等式具有放縮功能,常常用于證明不等式,解決問題的關鍵是分析不等式兩邊的結構特點,選擇好切入點.
項和相類似;(3)觀測數列的特點形式,看使用什么方法求和.使用裂項法求和時,要注意正負項相消時消去了哪些項,保留了哪些項,切不可漏寫未被消去的項,未被消去的項有前后對稱的特點,實質上造成正負相消是此法的根源和目的;(4)不等式具有放縮功能,常常用于證明不等式,解決問題的關鍵是分析不等式兩邊的結構特點,選擇好切入點.
試題解析:解:(1)
 且
且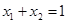
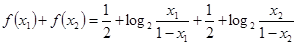
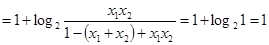
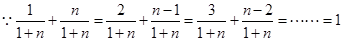
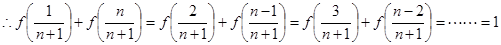

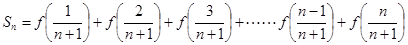
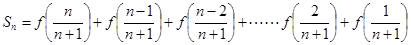
+(2)得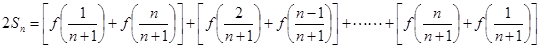
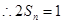 ,解得
,解得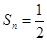
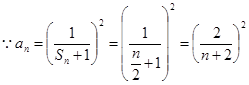
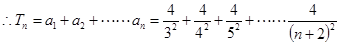
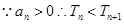 ,
,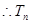 是單調遞減數列
是單調遞減數列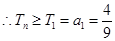
又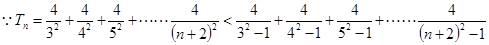
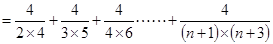
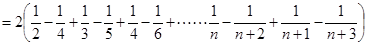
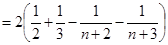

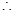 綜上所述:
綜上所述: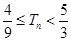
考點:(1)對數的運算性質;(2)倒序相加求數列的和;(3)證明不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com