
已知單調(diào)遞增的等比數(shù)列{an}滿足a1+a2+a3=14,且a2+1是a1,a3的等差中項.
(1)求數(shù)列{an}的通項公式;
(2)若bn=anlog2an,求數(shù)列{bn}的前n項和Sn;
(3)若存在n∈N*,使得Sn+1﹣2≤8n3λ成立,求實數(shù)λ的最小值.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析試題分析:
解題思路:(1)設(shè)出等比數(shù)列的首項與公比,列出關(guān)于 的方程組,解得即可;(2)由(1)得出
的方程組,解得即可;(2)由(1)得出 ,利用錯位相減法求和;(3)先進(jìn)行變量分離,轉(zhuǎn)化為求關(guān)于
,利用錯位相減法求和;(3)先進(jìn)行變量分離,轉(zhuǎn)化為求關(guān)于 的函數(shù)的最值問題.
的函數(shù)的最值問題.
規(guī)律總結(jié):涉及等差數(shù)列或等比數(shù)列的通項問題,往往列出關(guān)于基本量的方程組,進(jìn)而求出基本量,數(shù)列求和的方法主要有:倒序相加法、裂項抵消法、分組求和法、錯位相減法.
注意點:存在n∈N*,使得 成立,只需
成立,只需 ,而不是最大值.
,而不是最大值.
試題解析:(1)設(shè)等比數(shù)列 的公比為q,
的公比為q,
∵a1+a2+a3=14,且a2+1是a1,a3的等差中項,
∴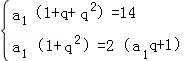 ,
,
解得q=2,a1=2,或q= ,a1=8(舍)
,a1=8(舍)
∴an=2n.
(2)bn=anlog2an=n•2n,
∴ ,①
,①
2Sn=1×22+2×23+3×24+…+n×2n+1,②
①﹣②,得
= ,
,
∴ .
.
(3)由(2)知 ,
,
原問題等價于:存在n∈N*,使得 成立,
成立,
令f(n)= ,只需λ≥f(n)min即可,
,只需λ≥f(n)min即可,
∵f(n+1)﹣f(n)= =
= ,
,
∴f(n+1)﹣f(n)的正負(fù)取決于n2﹣2n﹣1=(n﹣1)2﹣2的正負(fù),
∴f(1)>f(2)>f(3),f(3)<f(4)<…
∴f(n)min=f(3)= ,即
,即 ,
,
∴λ的最小值是 ..
..
考點:1.數(shù)列的通項公式;2.數(shù)列的前 項和.
項和.


科目:高中數(shù)學(xué) 來源: 題型:解答題
已知各項均為正數(shù)的等比數(shù)列{an}滿足a3 =8,a5 +a7=160,{an}的前n項和為Sn.
(1)求an;
(2)若數(shù)列{bn}的通項公式為bn=(-1)n·n(n∈N+),求數(shù)列{an·bn}的前n項和Tn。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè) 為數(shù)列
為數(shù)列 的前
的前 項和,對任意的
項和,對任意的 N,都有
N,都有
 為常數(shù),且
為常數(shù),且 .
.
(1)求證:數(shù)列 是等比數(shù)列;
是等比數(shù)列;
(2)設(shè)數(shù)列 的公比
的公比 與
與 函數(shù)關(guān)系為
函數(shù)關(guān)系為 ,數(shù)列
,數(shù)列 滿足
滿足 ,點
,點 落在
落在  上,
上, ,
, N,求數(shù)列
N,求數(shù)列 的通項公式;
的通項公式;
(3)在滿足(2)的條件下,求數(shù)列 的前
的前 項和
項和 ,使
,使
 恒成立時,求
恒成立時,求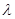 的最小值.[
的最小值.[
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某地今年年初有居民住房面積為 m2,其中需要拆除的舊房面積占了一半,當(dāng)?shù)赜嘘P(guān)部門決定每年以當(dāng)年年初住房面積的10%的住房增長率建設(shè)新住房,同時每年拆除xm2的舊住房,又知該地區(qū)人口年增長率為4.9‰.
m2,其中需要拆除的舊房面積占了一半,當(dāng)?shù)赜嘘P(guān)部門決定每年以當(dāng)年年初住房面積的10%的住房增長率建設(shè)新住房,同時每年拆除xm2的舊住房,又知該地區(qū)人口年增長率為4.9‰.
(1)如果10年后該地區(qū)的人均住房面積正好比目前翻一番,那么每年應(yīng)拆除的舊住房面積x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的舊房?
下列數(shù)據(jù)供計算時參考:
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列 的前
的前 項和為
項和為 滿足
滿足 (
(  )
)
(1)證明數(shù)列 為等比數(shù)列;
為等比數(shù)列;
(2)設(shè) ,求數(shù)列
,求數(shù)列 的前
的前 項和
項和
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com