
 ,
, ,函數
,函數 .
.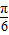 的范圍,然后利用函數的最值時的2x-
的范圍,然后利用函數的最值時的2x-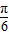 的值,即可得到單調增區間.
的值,即可得到單調增區間.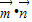 =
=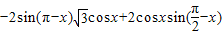
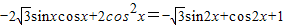 2分
2分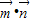 =
=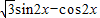 ,…(3分)
,…(3分)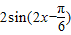 .…(4分)
.…(4分)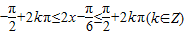 ,
,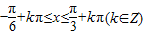 ,…(6分)
,…(6分)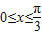 和
和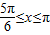 ,
,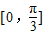 和
和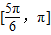 .…(8分)
.…(8分)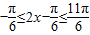 ,
,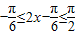 和
和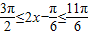 ,…(6分)
,…(6分)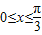 和
和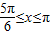 ,
,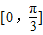 和
和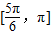 .…(8分)
.…(8分)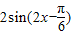 的圖象:g(x)=sinx的圖象向右平移
的圖象:g(x)=sinx的圖象向右平移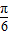 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 倍(縱坐標不變),最后把所得各點的縱坐標伸長為原來的2倍(橫坐標不變),得到f(x)=
倍(縱坐標不變),最后把所得各點的縱坐標伸長為原來的2倍(橫坐標不變),得到f(x)=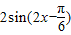 的圖象.…(14分)(每一步變換2分)
的圖象.…(14分)(每一步變換2分)

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2011屆廣東省實驗中學、華師附中、深圳中學、廣雅中學高三上學期期末數學文卷 題型:解答題
(本小題滿分12分)
已知向量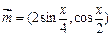 ,
, ,函數
,函數
(1)求 的最小正周期;
的最小正周期;
(2)若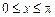 ,求
,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省六校教育研究會高三2月聯考理科數學試卷(解析版) 題型:解答題
已知向量 ,
, ,函數
,函數
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)在 中,設角
中,設角 ,
, 的對邊分別為
的對邊分別為 ,若
,若 ,且
,且 ?,求角
?,求角 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省五校高三下學期第二次聯考理科數學試卷(解析版) 題型:解答題
已知向量 ,
, ,函數
,函數 .
.
(Ⅰ)若方程 在
在 上有解,求
上有解,求 的取值范圍;
的取值范圍;
(Ⅱ)在 中,
中, 分別是A,B,C所對的邊,當(Ⅰ)中的
分別是A,B,C所對的邊,當(Ⅰ)中的 取最大值且
取最大值且 時,求
時,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2010年南安一中高一下學期期末考試數學卷 題型:解答題
(本小題滿分12分)
已知向量 ,
, ,函數
,函數 .
.
(1)求函數 的最小正周期以及單調遞增區間;
的最小正周期以及單調遞增區間;
(2)若 時, 求
時, 求 的值域;
的值域;
(3)求方程 在
在 內的所有實數根之和.
內的所有實數根之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com