
(1)求數(shù)列{an}的通項公式;
(2)記Tn=![]() (n>1,n∈N*),設(shè)g(n)=T2n+1-Tn+1,試確定實數(shù)m的取值范圍,使得對于一切大于1的自然數(shù)n,不等式g(n)>[logm(m-1)]2-
(n>1,n∈N*),設(shè)g(n)=T2n+1-Tn+1,試確定實數(shù)m的取值范圍,使得對于一切大于1的自然數(shù)n,不等式g(n)>[logm(m-1)]2-![]() 恒成立.
恒成立.
解:(1)由 得f(x-3)=x2-6x+8,從而f(x)=x2-1.
得f(x-3)=x2-6x+8,從而f(x)=x2-1.
∵f(a-1),1,f(a+1)是一個遞增的等差數(shù)列{an}的前三項,
∴f(a-1)+f(a+1)=2,
即(a2-2a)+(a2+2a)=2.
解得a=-1或a=1.
若a=-1,則a1=3,a3=-1不合題意.
若a=1,則a1=-1,a3=3.從而數(shù)列{an}的公差為d=2,
an=-1+(n-1)2=2n-3.
(2)∵Tn=![]() (n>1,n∈N*),
(n>1,n∈N*),
∴g(n)=T2n+1-Tn+1=![]() .
.
又g(n+1)-g(n)=![]()
![]()
∴g(n+1)>g(n).∴g(n)是關(guān)于n的增函數(shù).
∴g(n)min=g(2)=![]() .
.
∴要使一切大于1的自然數(shù)n,不等式?g(n)>[logm(m-1)]2-![]() 恒成立,
恒成立,
只要![]() >[logm(m-1)]2-
>[logm(m-1)]2-![]() 成立即可.
成立即可.
由![]() 得m>1且m≠2,
得m>1且m≠2,
此時設(shè)[logm(m-1)]2=t,則t>0,
于是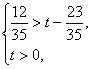 解得0<t<1.
解得0<t<1.
由此得0<[logm(m-1)]2<1,
解得m>![]() 且m≠2.
且m≠2.


科目:高中數(shù)學(xué) 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x+1 |
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 4 |
| 1 |
| 8 |
| 5 |
| 11 |
| 7 |
| 13 |
| 7 |
| 8 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2004全國各省市高考模擬試題匯編(天利38套)·數(shù)學(xué) 題型:013
若函數(shù)f(x)滿足f(x+1)= f(x),則f(x)的解析式在下列四式中只有可能是
f(x),則f(x)的解析式在下列四式中只有可能是
[ ]
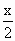

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:四川省成都樹德中學(xué)2012屆高考適應(yīng)考試(一)數(shù)學(xué)試題文理科 題型:022
對于函數(shù)f(x),定義:若存在非零常數(shù)M,T,使函數(shù)f(x)對定義域內(nèi)的任意x,都滿足f(x+T)-f(x)=M,則稱函數(shù)y=f(x)是準(zhǔn)周期函數(shù),非零常數(shù)T稱為函數(shù)y=f(x)的一個準(zhǔn)周期.如函數(shù)f(x)=2x+sinx是以T=2π為一個準(zhǔn)周期且M=4π的準(zhǔn)周期函數(shù).下列命題:
①2π是函數(shù)f(x)=sinx的一個準(zhǔn)周期;
②f(x)=x+(-1)x(x∈z)是以T=2為一個準(zhǔn)周期且M=2的準(zhǔn)周期函數(shù);
③函數(shù)f(x)=kx+b+Asin(wx+φ)(k≠0,w>0)是準(zhǔn)周期函數(shù);
④如果f(x)是一個一次函數(shù)與一個周期函數(shù)的和的形式,則f(x)一定是準(zhǔn)周期函數(shù);
⑤如果f(x+1)=-f(x)則函數(shù)h(x)=x+f(x)是以T=2為一個準(zhǔn)周期且M=4的準(zhǔn)周期函數(shù);其中的真命題是________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com