
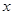 萬元投資甲項目,
萬元投資甲項目,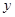 萬元投資乙項目,試寫出
萬元投資乙項目,試寫出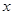 、
、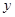 所滿足的條件,并在直角坐標系內做出表示
所滿足的條件,并在直角坐標系內做出表示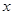 、
、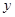 范圍的圖形;
范圍的圖形;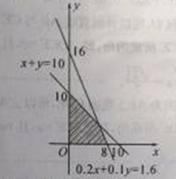 ;
;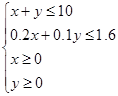 ,再在平面直角坐標系中畫出對應的可行域,注意邊界上的點也滿足條件;(2)主要是利用可行域求解線性目標函數的最大值即得投資公司獲得的最大利潤,圖解法解決含有實際背景的線性規劃問題的基本步驟是:①列出約束條件,確定目標函數;②畫出不等式(組)表示的平面區域;③作平行直線系使之與可行域有交點,求得最優解;④寫出目標函數的最值,并下結論.
,再在平面直角坐標系中畫出對應的可行域,注意邊界上的點也滿足條件;(2)主要是利用可行域求解線性目標函數的最大值即得投資公司獲得的最大利潤,圖解法解決含有實際背景的線性規劃問題的基本步驟是:①列出約束條件,確定目標函數;②畫出不等式(組)表示的平面區域;③作平行直線系使之與可行域有交點,求得最優解;④寫出目標函數的最值,并下結論.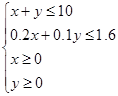 上述不等式組表示的平面區域如圖中陰影部分(含邊界),
上述不等式組表示的平面區域如圖中陰影部分(含邊界),
 ,作直線
,作直線 ,并作平行于直線
,并作平行于直線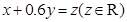 與可行域相交,當平行直線經過直線
與可行域相交,當平行直線經過直線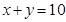 與
與 的交點
的交點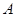 時,其截距最大,解方程組
時,其截距最大,解方程組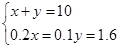 ,解得
,解得 ,即
,即 ,
,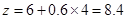 (萬元),
(萬元), 當
當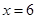 ,
,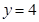 時,
時, 取得最大值.
取得最大值.


科目:高中數學 來源:不詳 題型:填空題
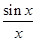 在點M(π,0)處的切線與兩坐標軸圍成的三角形區域為D(包含三角形內部與邊界).若點P(x,y)是區域D內的任意一點,則x+4y的最大值為 .
在點M(π,0)處的切線與兩坐標軸圍成的三角形區域為D(包含三角形內部與邊界).若點P(x,y)是區域D內的任意一點,則x+4y的最大值為 .查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
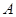 、
、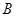 兩類產品,甲種設備每天能生產
兩類產品,甲種設備每天能生產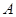 類產品
類產品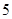 件和
件和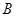 類產品
類產品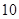 件,乙種設備每天能生產
件,乙種設備每天能生產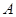 類產品
類產品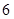 件和
件和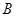 類產品
類產品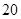 件.已知設備甲每天的租賃費為
件.已知設備甲每天的租賃費為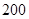 元,設備乙每天的租賃費為
元,設備乙每天的租賃費為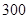 元,現該公司至少要生產
元,現該公司至少要生產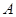 類產品
類產品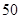 件,
件,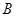 類產品
類產品 件,所需租賃費最少為____元.
件,所需租賃費最少為____元.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com