如圖,在棱長為2的正方體ABCD-A
1B
1C
1D
1中,E為棱CC
1的中點。
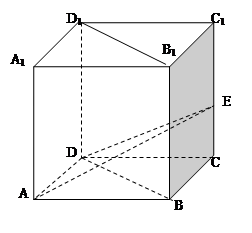
(1)求證:BD⊥AE;
(2)求點A到平面BDE的距離.
(1)詳見解析,(2)

試題分析:(1)證明線線垂直,有兩個思路,一是在平面幾何中利用勾股定理,二是利用線面垂直轉(zhuǎn)化.而異面直線垂直只能利用線面垂直轉(zhuǎn)化.因為AC⊥BD,所以證明思路為證明BD⊥面ACE,而關鍵CC1⊥BD就可得到證明.(2)求點A到平面BDE的距離也有兩個思路,一是作出A到平面BDE的距離,即垂線段,二是利用體積求高.本題作出A到平面BDE較為復雜,所以優(yōu)先考慮利用體積求高.因為

,所以


試題解析:(1)連結(jié)AC

ABCD-A1B1C1D1是正方體,

AC⊥BD,CC1⊥ABCD
又

BD

面ABCD,

CC1⊥BD
又

AC

C1C=C,

BD⊥面ACE
又

AE

面ACE,

BD⊥AE
(2)設A到面BDE的距離為h

正方體的棱長為2,E為C1C中點,



練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
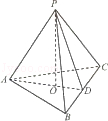
(2011•浙江)如圖,在三棱錐P﹣ABC中,AB=AC,D為BC的中點,PO⊥平面ABC,垂足O落在線段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)證明:AP⊥BC;
(2)在線段AP上是否存在點M,使得二面角A﹣MC﹣β為直二面角?若存在,求出AM的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐
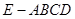
中,底面

為正方形,
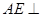
平面
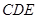
,已知
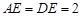
,
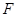
為線段
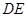
的中點.
(1)求證:
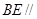
平面
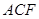
;
(2)求二面角
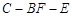
的平面角的余弦值.
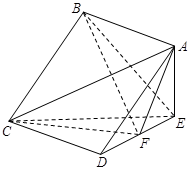
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,且

底面ABCD,
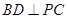
,E是PA的中點.

(1)求證:平面
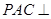
平面EBD;
(2)若PA=AB=2,求三棱錐P-EBD的高.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在三棱錐
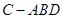
中,
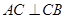
,
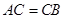
,
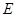
為
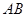
的中點,
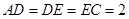
,
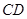
=
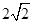
.
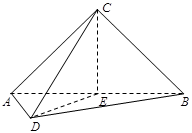
(1)求證:平面
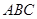
⊥平面
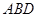
;
(2)求直線
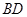
與平面
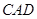
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在空間四邊形
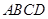
中,

分別是
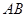
和
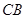
上的點,
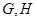
分別是
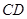
和

上的點,且
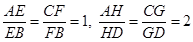
,求證:
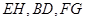
三條直線相交于同一點.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設a,b為兩條不同的直線,
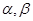
為兩個不同的平面,則下列說法正確的是( )
| A.若a∥α,α⊥β,則a∥β | B.若a∥b,a⊥β,則b⊥β |
| C.若a∥α,b∥α,則a∥b | D.若a⊥b,a∥α,則b⊥α |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
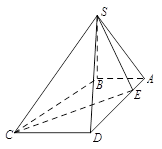
如圖,在四棱錐
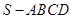
中,
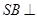
底面

.底面

為梯形,

,
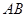
∥

,
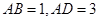
,

.若點
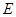
是線段
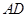
上的動點,則滿足

的點
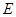
的個數(shù)是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知集合
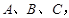
且
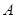
={直線},
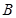
={平面},
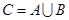
,若
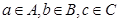
,有四個命題①
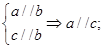
②
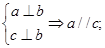
③

④
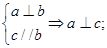
其中所有正確命題的序號是( )
查看答案和解析>>



 ,所以
,所以

 ABCD-A1B1C1D1是正方體,
ABCD-A1B1C1D1是正方體, AC⊥BD,CC1⊥ABCD
AC⊥BD,CC1⊥ABCD BD
BD 面ABCD,
面ABCD, CC1⊥BD
CC1⊥BD AC
AC C1C=C,
C1C=C, BD⊥面ACE
BD⊥面ACE AE
AE 面ACE,
面ACE, BD⊥AE
BD⊥AE 正方體的棱長為2,E為C1C中點,
正方體的棱長為2,E為C1C中點,





 底面ABCD,
底面ABCD,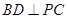 ,E是PA的中點.
,E是PA的中點.
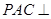 平面EBD;
平面EBD;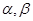 為兩個不同的平面,則下列說法正確的是( )
為兩個不同的平面,則下列說法正確的是( )