Question

（04年福建卷理）（12分）

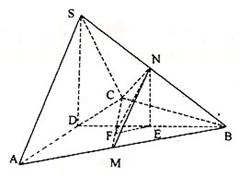
在三棱錐S-ABC中，△ABC是邊長為4的正三角形，平面SAC⊥平面ABC，SA=SC=2，M、N分別為AB、SB的中點。

（Ⅰ）證明：AC⊥SB；

（Ⅱ）求二面角N-CM-B的大小；

（Ⅲ）求點B到平面CMN的距離。

 

Answer 1

解析：解法一：（Ⅰ）取AC中點D，連結(jié)SD、DB.

∵SA=SC，AB=BC，

∴AC⊥SD且AC⊥BD，

∴AC⊥平面SDB，又SB平面SDB，

∴AC⊥SB.

（Ⅱ）∵AC⊥平面SDB，AC平面ABC，

∴平面SDB⊥平面ABC.

過N作NE⊥BD于E，NE⊥平面ABC，過E作EF⊥CM于F，連結(jié)NF，

則NF⊥CM.

∴∠NFE為二面角N-CM-B的平面角.

∵平面SAC⊥平面ABC，SD⊥AC，∴SD⊥平面ABC.

又∵NE⊥平面ABC，∴NE∥SD.

∵SN=NB，∴NE=SD===，且ED=EB.

在正△ABC中，由平幾知識可求得EF=MB=，

在Rt△NEF中，tan∠NFE==2，

∴二面角N-CM-B的大小是arctan2.

（Ⅲ）在Rt△NEF中，NF==，

∴S_△CMN=CM?NF=，S_△CMB=BM?CM=2.

設(shè)點B到平面CMN的距離為h，

∵V_B-CMN=V_N-CMB，NE⊥平面CMB，∴S_△CMN?h=S_△CMB?NE，

∴h==.即點B到平面CMN的距離為.

解法二：（Ⅰ）取AC中點O，連結(jié)OS、OB.

∵SA=SC，AB=BC，

∴AC⊥SO且AC⊥BO.

∵平面SAC⊥平面ABC，平面SAC∩平面ABC=AC

∴SO⊥面ABC，∴SO⊥BO.

如圖所示建立空間直角坐標(biāo)系O-xyz.

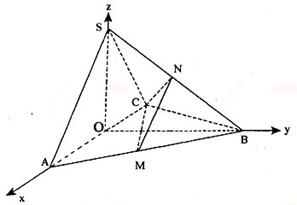
則A（2，0，0），B（0，2，0），C（-2，0，0），S（0，0，2），M(1，，0)，N(0，，).

∴=（-4，0，0），=（0，2，2），

∵?=（-4，0，0）?（0，2，2）=0，

∴AC⊥SB.

（Ⅱ）由（Ⅰ）得=（3，，0)，=（-1，0，）.設(shè)n=（x，y，z）為平面CMN的一個法向量，

則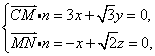取z=1，則x=，y=-，

∴n=(，-，1)，

又=(0，0，2)為平面ABC的一個法向量，

∴cos(n，)==.

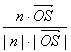∴二面角N-CM-B的大小為arccos.

（Ⅲ）由（Ⅰ）（Ⅱ）得=（-1，，0），n=（，-，1）為平面CMN的一個法向量，

∴點B到平面CMN的距離d==.