
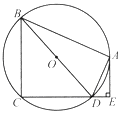
如圖,四邊形ABCD內接于⊙ ,
,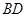 是⊙
是⊙ 的直徑,
的直徑,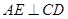 于點
于點 ,
, 平分
平分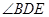 .
.
(Ⅰ)證明: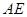 是⊙
是⊙ 的切線
的切線
(Ⅱ)如果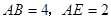 ,求
,求 .
.
(Ⅰ)見解析(Ⅱ)
解析試題分析:(Ⅰ)連結OA,由OA=AD知∠OAD=∠ODA,由 平分
平分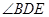 知,∠BDA=∠ADE,所以∠ADE=∠OAD,由內錯角相等兩直線平行得OA∥CE,因為AE⊥CE,所以OA⊥AE,故AE是圓O的切線;(Ⅱ)由(Ⅰ)可得△ADE∽△BDA,所以
知,∠BDA=∠ADE,所以∠ADE=∠OAD,由內錯角相等兩直線平行得OA∥CE,因為AE⊥CE,所以OA⊥AE,故AE是圓O的切線;(Ⅱ)由(Ⅰ)可得△ADE∽△BDA,所以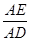 =
=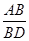 ,即BD=2AD,所以所以∠ABD=30°,從而∠DAE=30°,在直角三角形AED中,求出DE,再由切割線定理得AE2=ED·EC=ED·(CD+DE),即可求得CD的值.
,即BD=2AD,所以所以∠ABD=30°,從而∠DAE=30°,在直角三角形AED中,求出DE,再由切割線定理得AE2=ED·EC=ED·(CD+DE),即可求得CD的值.
試題解析:(Ⅰ)連結OA,則OA=OD,所以∠OAD=∠ODA,
又∠ODA=∠ADE,所以∠ADE=∠OAD,所以OA∥CE.
因為AE⊥CE,所以OA⊥AE.
所以AE是⊙O的切線. 5分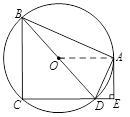
(Ⅱ)由(Ⅰ)可得△ADE∽△BDA,
所以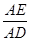 =
=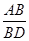 ,即
,即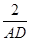 =
=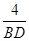 ,則BD=2AD,
,則BD=2AD,
所以∠ABD=30°,從而∠DAE=30°,
所以DE=AEtan30°=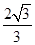 .
.
由切割線定理,得AE2=ED·EC,
所以4=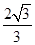 (
(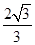 +CD),所以CD=
+CD),所以CD= . 10分
. 10分
考點:切線的判定,相似三角形的判定與性質,切割線定理.


科目:高中數學 來源: 題型:填空題
如圖1,在平面直角坐標系中,邊長為1的正方形OABC的頂點B在 軸的正半軸上,O為坐標原點.現將正方形OABC繞O點按順時針方向旋轉.
軸的正半軸上,O為坐標原點.現將正方形OABC繞O點按順時針方向旋轉.
(1)當點A第一次落到 軸正半軸上時,求邊BC在旋轉過程中所掃過的面積;
軸正半軸上時,求邊BC在旋轉過程中所掃過的面積;
(2)若線段AB與 軸的交點為M(如圖2),線段BC與直線
軸的交點為M(如圖2),線段BC與直線 的交點為N.設
的交點為N.設 的周長為
的周長為 ,在正方形OABC旋轉的過程中
,在正方形OABC旋轉的過程中 值是否有改變?并說明你的結論;
值是否有改變?并說明你的結論;
(3)設旋轉角為 ,當
,當 為何值時,
為何值時, 的面積最小?求出這個最小值, 并求出此時△BMN的內切圓半徑.
的面積最小?求出這個最小值, 并求出此時△BMN的內切圓半徑.

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
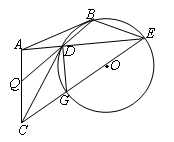
如圖,已知圓 內接四邊形
內接四邊形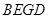 ,
, 切圓
切圓 于點
于點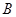 ,且與四邊形
,且與四邊形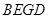 對角線
對角線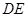 延長線交于點
延長線交于點 ,
, 切圓O于點
切圓O于點 ,且與
,且與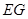 延長線交于點
延長線交于點 ,延長
,延長 交
交 于點
于點 ,若
,若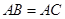 .
.
(1)求證: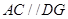 ;
;
(2)求證: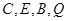 四點共圓.
四點共圓.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在△ABC中,CD是∠ACB的角平分線,△ADC的外接圓交BC于點E,AB=2AC
(1)求證:BE=2AD;
(2)當AC=3,EC=6時,求AD的長.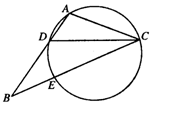
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com